Formel zur Berechnung der Höhe in regelmäßigen, gleichschenkligen, gleichseitigen und rechtwinkligen Dreiecken

Die Höhe eines Dreiecks ist eine wichtige Gerade und steht in engem Zusammenhang mit vielen Problemen der ebenen Geometrie. Was ist also die Höhe eines Dreiecks und wie berechnet man sie? Die Antwort und die einfachste Formel zur Berechnung der Höhe eines Dreiecks finden Sie im folgenden Artikel.

Inhaltsverzeichnis

• Formel zur Berechnung der Höhe in einem Dreieck
  • Berechnen Sie die Höhe in einem regelmäßigen Dreieck
  • Berechnen Sie die Höhe in einem gleichseitigen Dreieck
  • Formel zur Berechnung der Höhe in einem rechtwinkligen Dreieck
  • Formel zur Berechnung der Höhe in einem gleichschenkligen Dreieck
• Definition der Höhe in einem Dreieck
• Eigenschaften der drei Höhen eines Dreiecks

Formel zur Berechnung der Höhe in einem Dreieck

Berechnen Sie die Höhe in einem regelmäßigen Dreieck

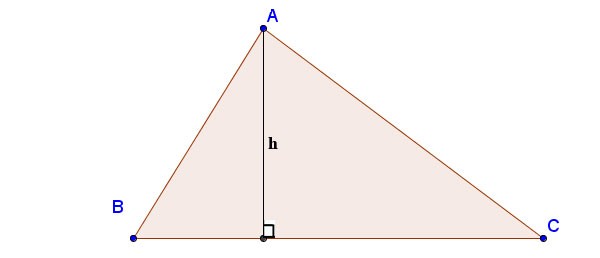
So berechnen Sie die Höhe eines Dreiecks mit der Heron-Formel:

Dabei sind a, b und c die Längen der Seiten; ha ist die Höhe vom Scheitelpunkt A zur Seite BC; p ist der Halbumfang:

Zum Beispiel: 

Gegeben sei das Dreieck ABC, Seite AB = 4 cm, Seite BC = 7 cm, Seite AC = 5 cm. Berechnen Sie die Höhe AH von A, das BC bei H schneidet, und berechnen Sie die Fläche von ABC.

Preis:

Halber Umfang des Dreiecks: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8 (cm)

Höhe   

=>

Betrachten wir das Dreieck ABC, haben wir:

Also,

Berechnen Sie die Höhe in einem gleichseitigen Dreieck

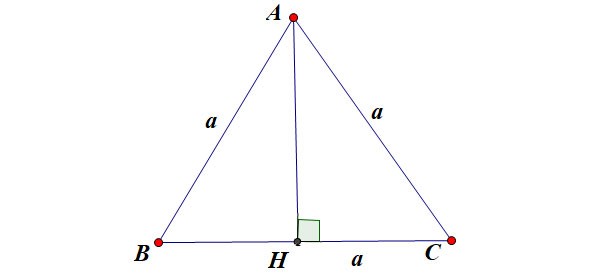
Angenommen, das gleichseitige Dreieck ABC hat die Seitenlänge a, wie in der Abbildung gezeigt:

Darin:

• h ist die Höhe eines gleichseitigen Dreiecks
• a ist die Seitenlänge eines gleichseitigen Dreiecks

Formel zur Berechnung der Höhe in einem rechtwinkligen Dreieck

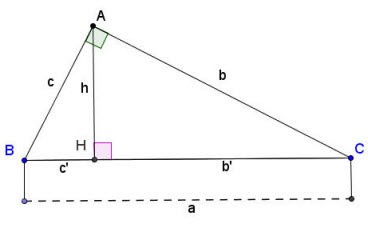
Angenommen, genau bei A befindet sich ein rechtwinkliges Dreieck ABC, wie oben gezeigt:

Formel zur Berechnung von Seiten und Höhen in einem rechtwinkligen Dreieck:

1. a2 = b2 + c2

2. b2 = ab′ und c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Darin:

• a, b, c sind die Seiten eines rechtwinkligen Dreiecks, wie oben gezeigt;
• b' ist die Projektion der Kante b auf die Hypothenuse;
• c' ist die Projektion der Kante c auf die Hypothenuse;
• h ist die Höhe eines rechtwinkligen Dreiecks, das vom Scheitelpunkt des rechten Winkels A bis zur Hypothenuse BC gezogen wird.

Beispiel 1: Gegeben ist ein Dreieck ABC mit rechtem Winkel zu A und einer Höhe von AH. Berechnen Sie BC, AC und AH, wobei AB = 15 cm und HC = 16 cm gilt.

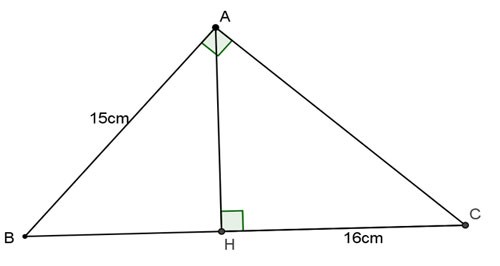
Preis:

Wenn wir die algebraische Formel im rechtwinkligen Dreieck ABC anwenden, erhalten wir:

AC2 = CH.BC = 16.BC

Nach dem Satz des Pythagoras gilt für das rechtwinklige Dreieck ABC mit dem rechten Winkel A:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 oder BC = -9 (eliminieren)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Betrachten Sie das rechtwinklige Dreieck ABC mit: AH.BC = AB.AC (geometrische Formel)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Also BC=25 (cm); AC=20 (cm); AH=12 (cm)

Beispiel 2 :

Das gegebene Dreieck ABC liegt genau bei A, AB = 24 cm, AC = 32 cm. Die Mittelsenkrechte von BC schneidet AC, BC in der Reihenfolge D und E. Berechnen Sie DE.

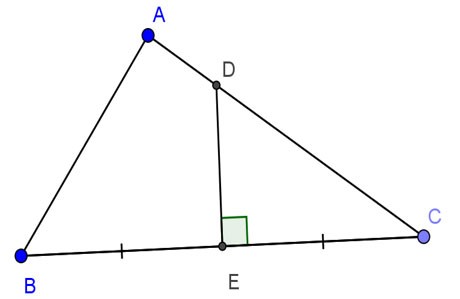
Preis:

Betrachten wir das rechtwinklige Dreieck ABC. Wir haben:

BC2 = AB2 + AC2 (gemäß dem Satz des Pythagoras)

BC2 = 242 + 322

BC2 = 1600

BC = 40 (cm)

EC = BC : 2 = 40 : 2 = 20 (cm)

Betrachten Sie das rechtwinklige Dreieck ACB und das rechtwinklige Dreieck ECD mit:

Es gilt ∠A = ∠E = 90°

∠C gemeinsam

=> Dreieck ACB ∾ Dreieck ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Also ED = 15 cm

Formel zur Berechnung der Höhe in einem gleichschenkligen Dreieck

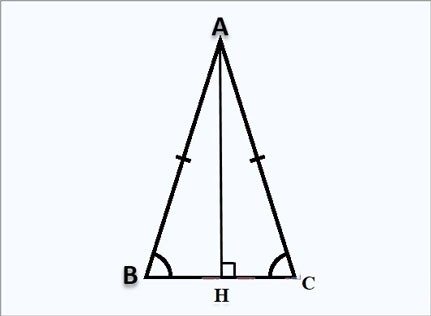
Angenommen, Sie haben ein gleichschenkliges Dreieck ABC bei A, die Höhe AH ist senkrecht bei H, wie oben gezeigt:

Formel zur Berechnung der Höhe AH:

Da das Dreieck ABC an der Stelle A gleichschenklig ist, ist die Höhe AH auch die Medianhöhe, also:

⇒ HB=HC=½BC

Wenn wir den Satz des Pythagoras im rechtwinkligen Dreieck ABH direkt bei H anwenden, erhalten wir:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Beispiel : Gegeben: Δ ABC ist an der Stelle A gleichschenklig, BC = 30 (cm), Höhe AH = 20 (cm). Berechnen Sie die Höhe, die der Seite dieses gleichschenkligen Dreiecks entspricht.

Lösung: Bedenken Sie, dass Δ ABC an der Stelle A gleichschenklig ist und BC = 30 (cm) ist.

⇒ BH = CH = 15 (cm).

Wenn wir den Satz des Pythagoras anwenden, erhalten wir:

Jetzt müssen wir BK = ? berechnen.

Wir haben:

Auf der anderen Seite

Daher haben wir ⇔

Definition der Höhe in einem Dreieck

Die Höhe eines Dreiecks ist ein senkrechtes Segment, das von einem Scheitelpunkt zur gegenüberliegenden Seite gezogen wird. Die gegenüberliegende Seite wird als Basis bezeichnet, zu der die Höhe gezogen wird. Die Länge der Höhe ist der Abstand zwischen Scheitelpunkt und Basis.

Eigenschaften der drei Höhen eines Dreiecks

Die drei Höhen eines Dreiecks verlaufen durch denselben Punkt. Dieser Punkt wird als Höhenschnittpunkt des Dreiecks bezeichnet .

Sie müssen lediglich die unbekannten Komponenten in den obigen Formeln zur Berechnung der Höhe eines Dreiecks berechnen, um die Höhe eines Dreiecks berechnen zu können.

• Was ist der Schwerpunkt? Formel zur Berechnung des Schwerpunkts eines Dreiecks