Die Formel zur Berechnung von Fläche und Umfang eines Parallelogramms gehört zum Grundwissen. Bitte beachten Sie die unten stehende Formel, die Quantrimang.com zusammengestellt hat.
Inhaltsverzeichnis
1. Fläche des Parallelogramms
Die Fläche eines Parallelogramms wird anhand der Größe der Oberfläche gemessen, also des sichtbaren flachen Teils des Parallelogramms.
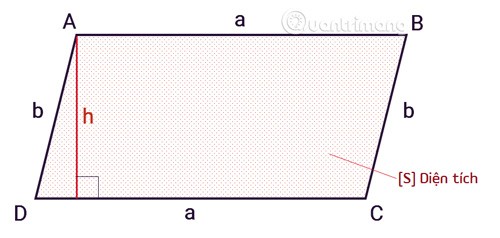
Die Fläche eines Parallelogramms berechnet sich nach der Formel gleich dem Produkt aus Basis mal Höhe.
SABCD = axh
Darin:
Sist die Fläche eines Parallelogramms.aist die Basis des Parallelogramms.hist die Höhe eines Parallelogramms von der Spitze bis zur Basis.
2. Umfang des Parallelogramms
Der Umfang eines Parallelogramms wird berechnet, indem die Länge der Linien, die die Form umgeben, und die Linie, die die gesamte Fläche umgibt, zum Doppelten der Summe aller Paare benachbarter Seiten addiert werden.
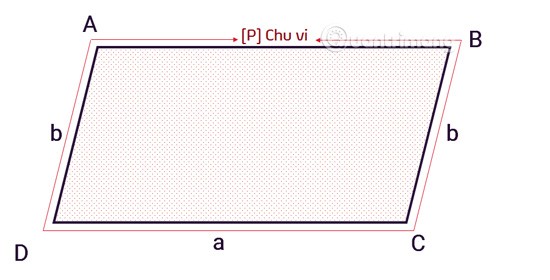
Mit anderen Worten: Der Umfang eines Parallelogramms ist die Summe der Längen seiner vier Seiten. Die genaue Formel lautet:
C = 2 x (a+b)
Darin:
Cist der Umfang eines Parallelogramms.aund bsind benachbarte Seiten eines Parallelogramms.
3. Was ist ein Parallelogramm?
Definieren
Ein Parallelogramm ist ein Viereck mit zwei Paaren paralleler Seiten oder einem Paar paralleler und gleich langer Seiten. Ein Parallelogramm hat zwei gleich große, gegenüberliegende Winkel und zwei Diagonalen, die sich in der Mitte der Form schneiden.
Ein Parallelogramm kann als Sonderfall eines Trapezes betrachtet werden.
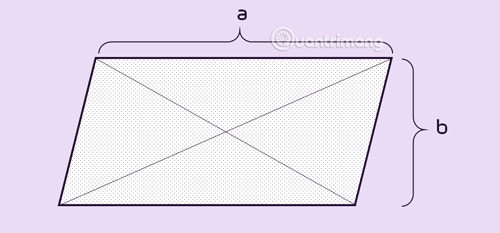
Eigenschaften des Parallelogramms
Im Parallelogramm:
- Gegenüberliegende Seiten sind gleich.
- Gegenüberliegende Winkel sind gleich.
- In der Mitte jeder Linie schneiden sich zwei Diagonalen.
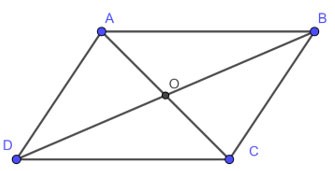
ABCD ist ein Parallelogramm, AC schneidet BD in O. Dann:
• AB = CD, AD = BC
•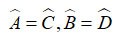
• OA = OC, OB = OD
Zeichen der Anerkennung
a) Ein Viereck mit parallelen gegenüberliegenden Seiten ist ein Parallelogramm.
b) Ein Viereck mit gleich langen gegenüberliegenden Seiten ist ein Parallelogramm.
c) Ein Viereck mit zwei gegenüberliegenden parallelen und gleich langen Seiten ist ein Parallelogramm.
d) Ein Viereck mit einander gegenüberliegenden, gleich großen Winkeln ist ein Parallelogramm.
e) Ein Viereck mit zwei Diagonalen, die sich jeweils in der Mitte schneiden, ist ein Parallelogramm.
4. Multiple-Choice-Fragen zur Überprüfung von Parallelogrammen
Übung 1 : Wählen Sie den falschen Satz.
A. Ein Parallelogramm hat zwei Diagonalen, die sich jeweils im Mittelpunkt schneiden.
B. Parallelogramm hat zwei gleich große gegenüberliegende Winkel
C. Ein Parallelogramm hat zwei Diagonalen, die senkrecht zueinander stehen.
D. Zwei Parallelogramme haben zwei Paare paralleler, gegenüberliegender Seiten.
Lösung
Im Parallelogramm:
+ Parallelogramm hat gegenüberliegende Seiten parallel
+ Gegenüberliegende Seiten sind gleich
+ Zwei Diagonalen schneiden sich in der Mitte jeder Linie, daher ist C falsch.
Die richtige Antwort ist: C
Aufgabe 2 : Gegeben sei das Parallelogramm ABCD mit  = α > 900. Zeichnen Sie die gleichseitigen Dreiecke ADE und ABF außerhalb des Parallelogramms. Was für ein Dreieck ist das Dreieck CEF? Wählen Sie die korrekteste Antwort.
A. Dreieck
B. Gleichschenkliges Dreieck
C. Gleichseitiges Dreieck
D. Stumpfes Dreieck
Antwort:
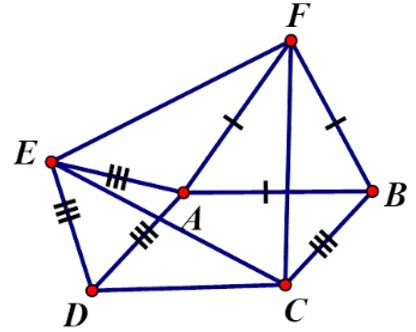

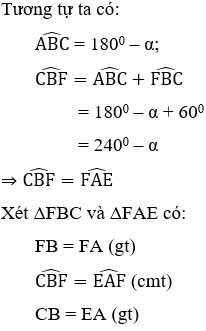
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
Aus (1) und (2) können wir folgern, dass CF = FE = EC, also ist das Dreieck CEF gleichseitig.
Lektion 3 : Wähle den falschen Satz. ABCD ist ein Parallelogramm. Dann:
A. AB = CD
B. AD = BC
C. Parallelogrammtest mit Antworten
D. AC = BD
Lösung
Im Parallelogramm:
+ Parallelogramm hat gegenüberliegende Seiten parallel
+ Gegenüberliegende Seiten sind gleich
+ Zwei Diagonalen schneiden sich in der Mitte jeder Linie, daher ist D falsch.
Lektion 4 : Füllen Sie die Lücke mit dem passenden Satz: „Ein Viereck mit zwei Diagonalen … ist ein Parallelogramm.“
A. gleich
B. schneiden
C. schneiden sich in der Mitte jeder Linie
D. parallel
Lösung
Zeichen:
Ein Viereck mit zwei Diagonalen, die sich jeweils in der Mitte schneiden, ist ein Parallelogramm.
Lektion 5 : Wählen Sie den falschen Satz:
A. Ein Viereck mit zwei Paaren paralleler, gegenüberliegender Seiten ist ein Parallelogramm.
B. Ein Trapez mit zwei gleichen Winkeln neben einer Basis ist ein Parallelogramm.
C. Ein Viereck mit zwei Paaren gleich großer gegenüberliegender Seiten ist ein Parallelogramm.
D. Ein Viereck mit zwei Paaren gleich großer, gegenüberliegender Winkel ist ein Parallelogramm.
Lösung
Zeichen:
+ Ein Viereck mit gegenüberliegenden parallelen Seiten ist ein Parallelogramm, also ist A richtig.
+ Ein Viereck mit gleich langen gegenüberliegenden Seiten ist ein Parallelogramm, also ist D richtig.
+ Ein Viereck mit einander gegenüberliegenden, gleichen Winkeln ist ein Parallelogramm, also ist D richtig.
Wenn man erkennt, dass ein Trapez mit zwei gleichen Winkeln neben einer Basis ein gleichschenkliges Trapez ist, ist B falsch.
Die richtige Antwort ist: B
5. Beispiele zur Berechnung von Umfang und Fläche eines Parallelogramms
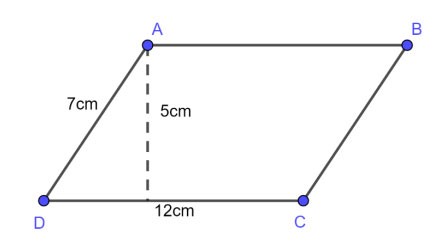
Beispiel 1 : Gegeben sei ein Parallelogramm mit einer Basislänge von 12 cm, einer Seitenlänge von 7 cm und einer Höhe von 5 cm. Berechnen Sie den Umfang und die Fläche dieses Parallelogramms?
Preis:
Der Umfang des Parallelogramms beträgt:
P = 2 x (12 + 7) = 38 (cm)
Die Fläche eines Parallelogramms beträgt:
S = axh = 12 x 5 = 60 (cm2)
Beispiel 2:
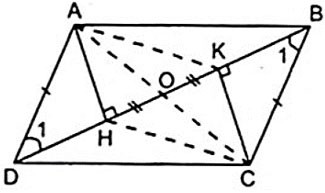
Gegeben sei das Parallelogramm ABCD, wobei H und K die Fußhöhen sind, die jeweils von den Eckpunkten A, C bis BD gezogen werden.
a) Beweisen Sie, dass AHCK ein Parallelogramm ist.
b) Sei O der Mittelpunkt von HK. Beweisen Sie, dass A, O und C kollinear sind.
Anweisen:
a) Aus der Hypothese folgt:
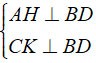 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
Wenn wir die Eigenschaften der Seiten von Parallelogrammen und die Eigenschaften der Wechselwinkel anwenden, erhalten wir:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(Hypotenuse – spitzer Winkel)
⇒ AH = CK (entsprechende Seiten sind gleich) ( 2 )
Aus (1) und (2) folgt, dass das Viereck AHCK mit gegenüberliegenden Seiten parallel und gleich groß ist und somit ein Parallelogramm darstellt.
b) Wenden Sie die Eigenschaften der Diagonalen des Parallelogramms AHCK an
Das Parallelogramm AHCK hat zwei Diagonalen, AC und HK, die sich jeweils in der Mitte schneiden. Da O der Mittelpunkt von HK ist, ist O auch der Mittelpunkt von AC.
⇒ A, O, C liegen auf einer Geraden.
Neben Parallelogrammen sind auch die Formeln zur Berechnung der Fläche und des Umfangs anderer gängiger geometrischer Formen wie Rauten , Quadrate , Trapeze , Rechtecke usw. sehr wichtig und finden in Studium und Leben breite Anwendung.
Hoffentlich haben Sie durch den obigen Artikel ein besseres Verständnis und Verständnis für die Grundlagen von Parallelogrammen erlangt. Hinterlassen Sie unten einen Kommentar, wenn Sie Fragen oder Anmerkungen haben, die Sie mit Quantrimang.com besprechen möchten.




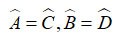



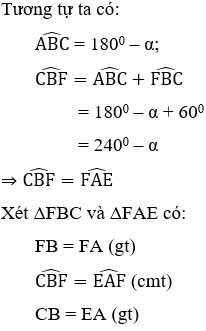


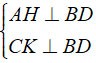 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK