Lernen Sie die Formel zur Berechnung der Mantelfläche, der Gesamtfläche und der Höhe eines Zylinders kennen, die Sie im Studium und im täglichen Leben anwenden können.
Inhaltsverzeichnis
So berechnen Sie die Fläche eines Zylinders
Die Fläche eines Zylinders setzt sich aus der Mantelfläche und der Gesamtfläche zusammen.
Sie können die Höhe und den Radius des Zylinders in die folgende Tabelle eingeben, um die Mantelfläche und die Gesamtfläche des Zylinders zu erfahren.
Formel zur Berechnung der Mantelfläche eines Zylinders
Die Mantelfläche eines Zylinders umfasst nur die Fläche der den Zylinder umgebenden Mantelfläche, nicht jedoch die Fläche der beiden Grundflächen.
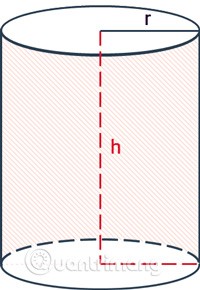
Die Formel zur Berechnung der Mantelfläche eines Zylinders lautet: Umfang des Grundkreises multipliziert mit der Höhe.
 |
Darin:
- Umgebung ist die Umgebung.
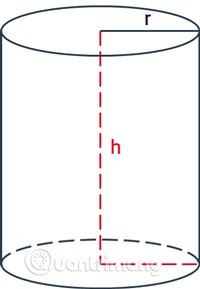
rist der Radius des Zylinders.hist die Höhe, der Abstand zwischen den beiden Grundflächen des Zylinders.
|
Beispiel: 1
Ein Kreiszylinder hat einen Basisradius von r = 5 cm und eine Höhe von h = 7 cm. Berechnen Sie die Mantelfläche des vertikalen Zylinders.
Lösung: Oberfläche eines Kreiszylinders: Sxq = 2.π.rh = 2π.5.7 = 70π = 219,8 (cm2).
Beispiel: 2
Gegeben sei das Quadrat ABCD mit der Seitenlänge 2a. O und O' seien die Mittelpunkte der Seiten AB bzw. CD. Dreht man das Quadrat um die Achse OO', entsteht ein Rotationszylinder. Berechnen Sie die Mantelfläche des Rotationszylinders.
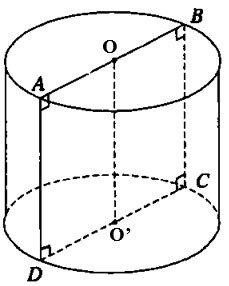
Lösung:
Der Radius des Grundkreises beträgt r= CD= a
Die Höhe des Zylinders beträgt h= OO'= AD=2a
Die Mantelfläche des Zylinders beträgt also Sxq = 2πrh = 2π.a.2a =4a2π
Formel zur Berechnung der Gesamtfläche eines Zylinders
Die Gesamtfläche errechnet sich aus der Größe der gesamten von der Figur eingenommenen Fläche, einschließlich der Mantelfläche und der Fläche der beiden kreisförmigen Grundflächen.
Die Formel zur Berechnung der Gesamtfläche eines Zylinders lautet: Mantelfläche plus Fläche der beiden Grundflächen.
Beispiel 1 : Berechnen Sie die Gesamtfläche eines Zylinders mit einer Basis von 3 und einer Höhe von 5.
Lösung:
Die Gesamtfläche beträgt Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Berechnen Sie die Höhe des Zylinders
Die Höhe eines Zylinders ist der Abstand zwischen den beiden Grundflächen des Zylinders.
Berechnen Sie die Höhe eines Zylinders, wenn Sie die Gesamtfläche und den Basisradius kennen
Beispiel: Gegeben sei ein Zylinder mit Basisradius R = 8 cm und einer Gesamtfläche von 564π cm². Berechnen Sie die Höhe des Zylinders.
Preis:
Wir haben
Berechnen Sie die Höhe eines Zylinders, wenn Sie die Mantelfläche kennen
=>
Formel zur Berechnung des Radius der Basis eines Zylinders
1. Formel zur Berechnung des Kreisumfangs; Fläche eines Kreises
Der Kreis hat einen Umfang C=2πr
=>
Der Kreis mit der Basis hat die Fläche S=πr2
=>
Beispiel. Berechnen Sie den Radius der Zylinderbasis in den folgenden Fällen:
a. Der Umfang des Basiskreises beträgt 6π
b. Die Fläche der Basis beträgt 25π
Lösung:
a. Der Radius des Grundkreises beträgt
b. Der Radius des Grundkreises beträgt
2. Die Basis ist der in das Polygon eingeschriebene Kreis
- Einbeschrieben in ein beliebiges Dreieck: wobei S die Fläche des Dreiecks und p der Halbumfang ist
- Eingeschrieben in ein gleichseitiges Dreieck: Seite
- Beschriftetes Quadrat:
Beispiel 1. Gegeben sei ein in einen Würfel einbeschriebener Zylinder mit der Kante a. Berechnen Sie den Radius des Zylinders.
Der Radius des Zylinders beträgt:
Beispiel 2. Gegeben sei ein regelmäßiges Prisma ABC.A'B'C' mit , dem umschriebenen Volumen des Zylinders. Berechnen Sie den Radius des Zylinders.
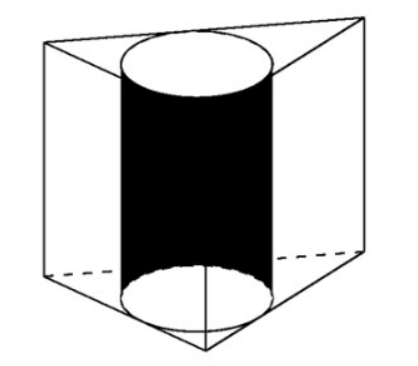
Das Volumen des Prismas beträgt
Die Basis eines regelmäßigen Prismas ist ein gleichseitiges Dreieck, also => die Seite
Daher beträgt der Radius der Zylinderbasis:
3. Die Basis ist der Kreis, der das Polygon umschreibt.
Umschrieben in einem beliebigen Dreieck:
Darin:
- a, b, c sind die Längen der drei Seiten des Dreiecks
- p ist der Halbumfang des Dreiecks:
Umfang eines rechtwinkligen Dreiecks: Hypothenuse
Umfang des gleichseitigen Dreiecks: Seite
Umfang des Quadrats: Seite
Zum Beispiel:
Berechnen Sie den Basisradius des Zylinders, der die regelmäßige Pyramide S.ABC umschreibt, in den folgenden Fällen:
a. ABC ist ein rechtwinkliges Dreieck an der Stelle A mit AB = a und AC = a√3
b. ABC hat AB= 5; AC= 7; BC=8
Preis:
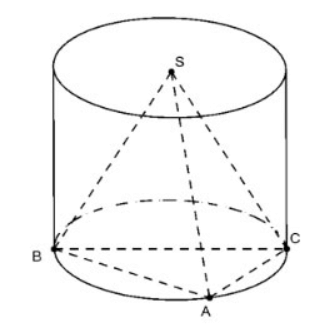
a. Hypothenuse
Da ABC ein rechter Winkel bei A ist, ist Radius R=0,5.BC=a
b. Der Halbumfang des Dreiecks ABC beträgt
Was ist ein Kreiszylinder?
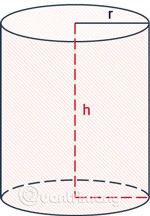
Ein Kreiszylinder ist ein Zylinder mit zwei gleich großen, parallel zueinander liegenden Kreisgrundflächen.
Zylinder werden häufig in Geometrieaufgaben von einfachen bis zu komplexen verwendet. Dabei wird häufig die Formel zur Berechnung von Fläche und Volumen eines Zylinders verwendet. Wenn Sie bereits wissen, wie man Fläche und Umfang eines Kreises berechnet, können Sie die Formeln zur Berechnung von Volumen, Mantelfläche und Gesamtfläche eines Zylinders leicht ableiten.
Formel zur Berechnung der Querschnittsfläche eines Zylinders
Schneiden Sie den Zylinder mit der Ebene (P) durch die Achse
- Der resultierende Querschnitt ist ein Rechteck.
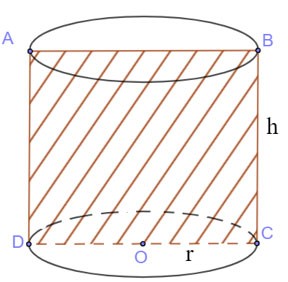 |
Querschnittsfläche:
SABCD = BC.CD =2r.h
|
Schneiden Sie den Zylinder durch die Ebene (P) parallel zur Achse und im Abstand x von ihr
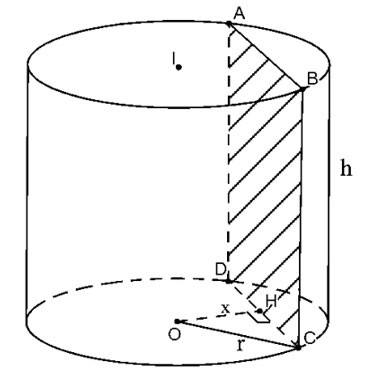 |
Der resultierende Querschnitt ist das Rechteck ABCD, wie oben gezeigt.
Sei H der Mittelpunkt von CD, dann gilt OH ⊥ CD=>
Daher ist die Querschnittsfläche
|
Schneiden Sie den Zylinder mit der Ebene (P), die nicht senkrecht zur Achse steht, sondern alle Mantellinien des Zylinders durchschneidet
 |
Der gebildete Querschnitt ist ein Kreis mit Mittelpunkt O' und Radius O'A'=r
Querschnittsfläche: S= πr2
|
Schneiden Sie den Zylinder mit der Ebene (P), die nicht senkrecht zur Achse steht, sondern alle Mantellinien des Zylinders durchschneidet.
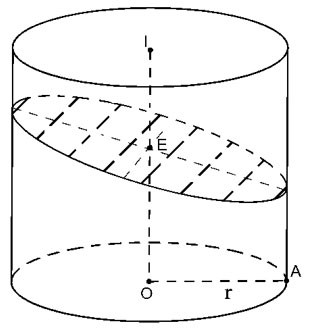 |
Der resultierende Querschnitt ist eine Ellipse (E) mit der Nebenachse 2r => a=r
Große Achse gleich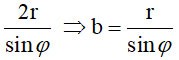
wobei 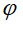 der Winkel zwischen der OI-Achse und (P) ist der Winkel zwischen der OI-Achse und (P) ist
Daher ist die Fläche S = π. ab =
|
Beispiel zur Berechnung der Fläche eines Zylinders
Lektion 1 :
Die Mantelfläche eines Zylinders hat einen kreisförmigen Basisumfang von 13 cm und eine Höhe von 3 cm.
Preis:
Wir haben: Kreisumfang C = 2R.π = 13cm, h = 3cm
Die Mantelfläche des Zylinders beträgt also:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Aufgabe 2 : Gegeben sei ein Zylinder mit einem Grundkreisradius von 6 cm und einer Höhe von 8 cm. Wie groß sind die Mantelfläche und die Gesamtfläche des Zylinders?
Preis
Gemäß der Formel beträgt die Grundfläche des Halbkreises r = 6 cm und die Höhe des Zylinders h = 8 cm. Daher ergibt sich die Formel zur Berechnung der Mantelfläche des Zylinders und der Gesamtfläche des Zylinders wie folgt:
Oberfläche des Zylinders = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Gesamtfläche des Zylinders = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Lektion 3 : Ein Zylinder hat einen Basisradius von 7 cm und eine Mantelfläche von 352 cm².
Dann beträgt die Höhe des Zylinders:
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Ein weiteres Ergebnis
Bitte wählen Sie die richtige Antwort aus.
Lösung: Wir haben
Antwort E ist also richtig.
Lektion 4 : Die Höhe eines Zylinders entspricht dem Radius des Grundkreises. Die Mantelfläche des Zylinders beträgt 314 cm². Berechne den Radius des Grundkreises und das Volumen des Zylinders (runde das Ergebnis auf die zweite Dezimalstelle).
Preis:
Die Mantelfläche des Zylinders beträgt 314cm2
Wir haben Sxq = 2.π.rh = 314
Wobei r = h
Also 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volumen des Zylinders: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Hoffentlich hat Ihnen der obige Artikel geholfen, grundlegende und fortgeschrittene Kenntnisse über Zylinder zu erlangen und die Gesamtfläche und Mantelfläche eines Zylinders zu berechnen.










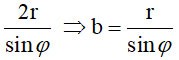
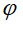 der Winkel zwischen der OI-Achse und (P) ist
der Winkel zwischen der OI-Achse und (P) ist