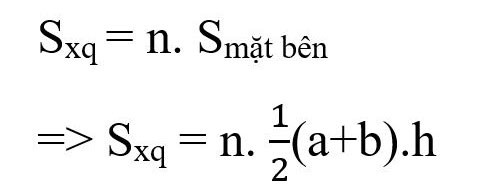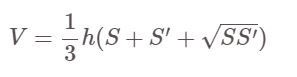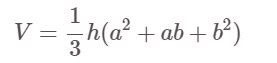Formel zur Berechnung des Volumens eines Pyramidenstumpfes, der Mantelfläche und der Gesamtfläche eines Pyramidenstumpfes

Im folgenden Artikel erfahren Sie, was ein Pyramidenstumpf ist, wie man das Volumen eines Pyramidenstumpfs berechnet, die Mantelfläche und die Gesamtfläche eines Pyramidenstumpfs.

Inhaltsverzeichnis

• Definition von frustum
  • Eigenschaften der Pyramidenstumpfform:
• Formel zur Berechnung der Fläche eines Pyramidenstumpfes
  • Oberfläche der Pyramidenstumpf 
  • Gesamtoberfläche einer Pyramidenstumpf
• Formel zur Berechnung des Volumens einer Pyramidenstumpf

Definition von frustum

Ein Pyramidenstumpf ist ein Teil eines Polyeders, der sich zwischen der Basis und dem Querschnitt befindet, der von einer Ebene parallel zur Basis der Pyramide geschnitten wird.

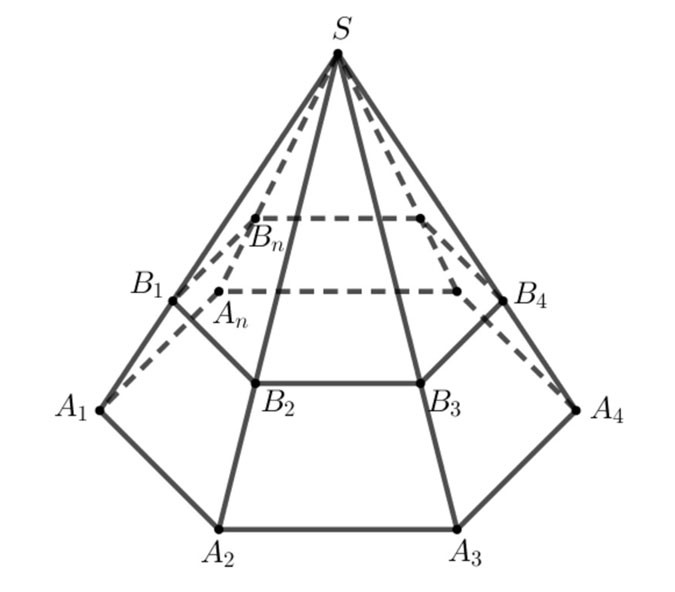
• Die Figur, die aus den Polygonen A1A2...An,B1B2...BnA1A2...An,B1B2...Bn und den Trapezen A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn besteht, wird als Pyramidenstumpf bezeichnet und als A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn bezeichnet.
• Einfach ausgedrückt wird aus der Pyramide S.A1A2...AnS.A1A2...An ein Pyramidenstumpf gebildet, nachdem die Pyramide S.B1B2...Bn.S.B1B2...Bn abgeschnitten wurde.

+ Die Polygone A1A2...An,B1B2...BnA1A2...An,B1B2...Bn heißen die beiden Basen,

+ Trapeze A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn werden als Seitenflächen bezeichnet.

+ Die Strecken A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn heißen Seitenkanten, die Kanten der Grundfläche heißen Basiskanten.

+ Der Abstand zwischen den beiden Grundflächen wird als Höhe des Pyramidenstumpfes bezeichnet.

Eigenschaften der Pyramidenstumpfform:

• Die beiden Grundflächen sind zwei Polygone (Dreiecke, Vierecke, Fünfecke usw.) mit entsprechenden parallelen Seiten und gleichen Seitenverhältnissen.
• Die Seitenflächen sind alle Trapeze.
• Die Linien, die die Seitenkanten enthalten, laufen in einem Punkt zusammen (der Spitze der Pyramide).
• Ein Pyramidenstumpf ist eine Pyramide, deren Grundflächen regelmäßige Polygone (mit gleich langen Seiten) sind. Daher sind die Seitenflächen eines Pyramidenstumpfs alle gleichschenklige Trapeze.

Formel zur Berechnung der Fläche eines Pyramidenstumpfes

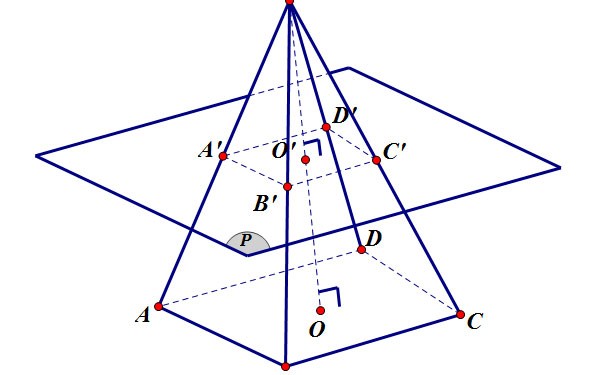
Oberfläche der Pyramidenstumpf

Die Mantelfläche eines Pyramidenstumpfes ist die Fläche der umgebenden Flächen, also des Teils, der den Pyramidenstumpf umgibt, abzüglich der Fläche der beiden Grundflächen.

So berechnen Sie die Mantelfläche eines Pyramidenstumpfes: Berechnen Sie die Fläche jeder Seitenfläche (Trapez) des Pyramidenstumpfes nach der Formel zur Berechnung der Fläche eines normalen Trapezes und berechnen Sie anschließend die Gesamtfläche.

Formel zur Berechnung der Fläche eines regelmäßigen Pyramidenstumpfes:

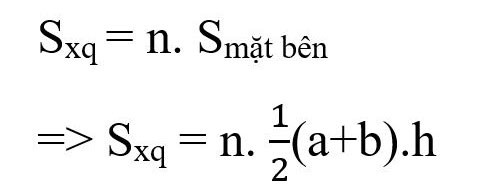
Darin:

• Sxq: Umgebung
• n: Anzahl der Seitenflächen des Pyramidenstumpfes (entspricht der Anzahl der Kanten des Grundpolygons)
• a, b: Seitenlängen der oberen bzw. unteren Basis
• h: Höhe der Seitenvierecke.

Beispiel 1: 

Berechnen Sie die Seitenfläche eines regelmäßigen vierseitigen Pyramidenstumpfes mit Basiskanten von 10 cm und 15 cm und einer Seitenhöhe von 12 cm.

Preis: 

Die Seitenfläche eines regelmäßigen vierseitigen Pyramidenstumpfes ist ein gleichschenkliges Trapez, daher beträgt die Fläche einer Seitenfläche:

Ein regelmäßiger vierseitiger Pyramidenstumpf hat 4 gleich lange Seiten, daher beträgt seine Seitenfläche:

150 x 4 = 600 (cm2)

Beispiel 2: Berechnen Sie die Mantelfläche eines regelmäßigen viereckigen Pyramidenstumpfes mit Basiskanten von 6 cm und 8 cm und einer Seitenhöhe von 5 cm. Berechnen Sie die Mantelfläche eines regelmäßigen viereckigen Pyramidenstumpfes mit Basiskanten von 6 cm und 8 cm.

Preis: 

Die Seitenfläche eines regelmäßigen vierseitigen Pyramidenstumpfes ist ein gleichschenkliges Trapez, daher ist die Fläche einer Seitenfläche gleich

Eine regelmäßige vierseitige Pyramidenstumpf hat vier gleich große Seiten, daher ist ihre Seitenfläche gleich

35 x 4 = 140 (cm2)

Gesamtoberfläche einer Pyramidenstumpf

Die Gesamtfläche eines Pyramidenstumpfes ist gleich der Summe der Mantelfläche und der Fläche der beiden Grundflächen.

Formel:                    Stp = Sxq + Großer Boden + Kleiner Boden

Darin:

• Stp: Gesamtfläche
• Sxq: Umgebung
• Große Basis: Große Grundfläche
• Kleine Basis: Kleine Grundfläche

Zum Beispiel: 

Berechnen Sie die Gesamtfläche eines regelmäßigen Pyramidenstumpfes anhand der in der Abbildung angegebenen Maße.

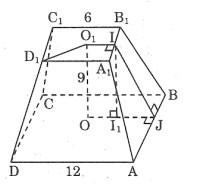
Preis:

Wir haben:

AD = 12 ⇒ ABl. = 6

Zeichnen Sie II1 ⊥ OJ, wir haben: I1J = 3

Wenn wir den Satz des Pythagoras auf das rechtwinklige Dreieck II1J anwenden, erhalten wir:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Somit:

Die Fläche einer Seite eines Trapezes beträgt:

Die Umgebungsfläche beträgt:

Die Fläche der oberen Basis beträgt: S = 6 x 6 = 36 (Einheiten)

Die Fläche der unteren Basis beträgt: S = 12 x 12 = 144 (Einheiten)

Die Gesamtfläche eines Pyramidenstumpfes beträgt:

Formel zur Berechnung des Volumens einer Pyramidenstumpf

Rezept:

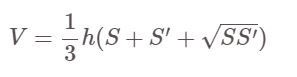
Darin:

• V: Volumen der Pyramidenstumpf
• S, S' sind die Flächen der großen bzw. kleinen Basis der Pyramide.
• h: Höhe der Pyramide, also der Abstand zwischen der großen und kleinen Basis

Ist ein Pyramidenstumpf ein Quadrat (regelmäßiges Viereck):

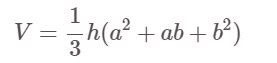
Darin:

• V: Lautstärke
• h: Höhe der Pyramide
• a, b sind die Längen der Kanten der großen Basis bzw. der kleinen Basis.