Was ist das Besondere an Edelstahl?
Edelstahl ist praktisch rostfrei, da seine chemische Zusammensetzung eine Schutzschicht auf seiner Oberfläche bildet und so den Kontakt des Eisens mit Sauerstoff verhindert.
Formel zur Berechnung der Trapezhöhe: regelmäßig, quadratisch, gleichschenklig
Ein Trapez ist ein konvexes Viereck mit zwei gegenüberliegenden parallelen Seiten. Diese werden als die beiden Grundflächen des Trapezes bezeichnet, die beiden übrigen Seiten sind die beiden Lateralseiten.
Die Höhe eines Trapezes ist der Abstand vom Scheitelpunkt der Senkrechten zur längsten Seite der Basis. Bei einem geraden Trapez entspricht die Höhe einer Seite des Trapezes.
Neben der Formel zur Berechnung der Fläche eines Trapezes , der Formel zur Berechnung des Umfangs eines Trapezes ist auch die Formel zur Berechnung der Höhe eines Trapezes sehr wichtig und steht im Zusammenhang mit vielen Problemen der ebenen Geometrie. Der folgende Artikel hilft Ihnen, die Formel zur Berechnung der Höhe eines regelmäßigen Trapezes, eines gleichschenkligen Trapezes und eines geraden Trapezes kennenzulernen.
Formel zur Berechnung der Trapezhöhe
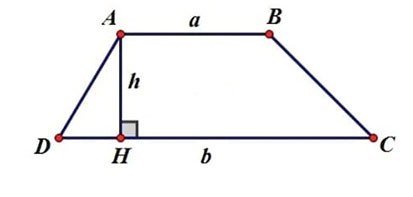
- h: Höhe des Trapezes
- S: Fläche des Trapezes
- a: Große Basislänge
- b: Länge der kleinen Basis
Die Formel zur Berechnung der Höhe eines Trapezes lautet: Fläche der beiden Basen multipliziert mit 2, geteilt durch die Gesamtlänge der beiden Basen.
Beispiel zur Berechnung der Höhe eines Trapezes
Beispiel 1 : Die Fläche eines Trapezes entspricht der Fläche eines Quadrats mit einer Seitenlänge von 30 cm. Die Gesamtlänge der größeren und der kleineren Basis beträgt 75 cm. Wie hoch ist das Trapez?
Preis:
Die Fläche eines Trapezes entspricht der Fläche eines Quadrats mit einer Seitenlänge von 30 cm, daher beträgt die Fläche des Trapezes: 30 x 30 = 900 cm2
Trapezhöhe beträgt: 900 x 2 : 75 = 24 cm
Beispiel 2 : Ein Trapez hat eine kleine Basis, die 60 % der großen Basis beträgt, also 24 cm weniger als die große Basis. Wie hoch ist das Trapez, wenn man bedenkt, dass seine Fläche 720 cm² beträgt?
Preis:
Die kleine Basis ist: 24 : (5 - 3) x 3 = 36 cm
Große Basis: 24 + 36 = 60
Trapezhöhe:
Warum ist es in einem Flugzeug immer kalt?
Haben Sie sich schon einmal gefragt, warum es in einem Flugzeug immer kalt ist, egal wie das Klima an Ihrem Zielort ist?
Chinas 20-Tage-Satellitenproduktionslinie
Die intelligente Produktionslinie in der fast 4.000 Quadratmeter großen Fabrik im nordchinesischen Tianjin nutzt neue Technologien zur Installation von Kabeln und verkürzt so die Satellitenproduktionszeit von einem halben Jahr auf 20 Tage.
Code Dai Nao O Long Vien, aktueller O Long Vien-Code
Code Dai Nao O Long Vien, O Long Vien Code unterstützt Spieler mit Spielwährung und Spieler werden dieses Online-Spiel definitiv attraktiver finden, wenn von Anfang an beim Einstieg ins Spiel Unterstützung vorhanden ist.
Neuester 3Q Summoner Code und wie man den Code einlöst
Das Spiel 3Q Summoner ist auch ein Spiel, das den Spielern attraktive Belohnungen durch Geschenkcodes bietet.
So registrieren Sie schnell ein DeepSeek-Konto
Die in China ansässige KI-App DeepSeek führt derzeit die App-Store-Charts an.
Microsoft Copilot verfügt über eine Copilot-Schaltfläche. So verwenden Sie sie
Windows Insider auf den Canary- und Dev-Kanälen werden nach der Veröffentlichung des Updates ein neues Copilot-Symbol in Paint sehen. Hier erfahren Sie, wie Sie es verwenden.
So lassen sich KI-Inhalte natürlicher klingen
Wordtune wurde 2017 eingeführt und stammt von AI21Labs, einem in Israel ansässigen Startup, das hauptsächlich an der Verarbeitung natürlicher Sprache und großen Sprachmodellen arbeitet.
Interessante Fakten über Brot, die Sie vielleicht nicht kennen
Brot ist nicht nur eines der Lieblingsspeisen vieler Menschen, es ist auch seit langem vor der Geschichtsschreibung Teil der menschlichen Kultur und Symbolik.
Interessante Fakten über Dinosaurier, die Sie vielleicht nicht kennen
Dinosaurier gehören zu den seltsamsten Tieren, die je auf diesem Planeten gelebt haben. Hier sind einige der erstaunlichsten Fakten über Dinosaurier, die Sie sich vorstellen können.
Devin, das KI-Tool, das automatisch Code schreiben kann
Ingenieure des Startups Cognition Labs haben gerade Devin auf den Markt gebracht, ein KI-Tool, das automatisch Code schreiben und ohne menschliches Eingreifen die Arbeit von Softwareentwicklern auf Rekrutierungsseiten wie Upwork übernehmen kann.
So vergleichen Sie Antivirensoftware vor dem Herunterladen
Die Wahl der richtigen Antivirensoftware ist wichtig, doch die Wahl des richtigen Antivirenprogramms ist nicht einfach. Es gibt viele Optionen, und jede behauptet, die beste zu sein.
So reinigen Sie Ihr Telefon sauber und sicher, um Covid 19 zu vermeiden
Um Ihr Telefon richtig und einfach von Corona zu reinigen, können Sie den Anweisungen in diesem Artikel folgen.
Lernen Sie Opera Air kennen: Operas neuer Browser
Viele Menschen sind skeptisch, wenn ein Webbrowser verspricht, den Geist zu entspannen. Doch Operas neuer Air-Browser ist überraschend nützlich und bietet praktische Tools zum Konzentrieren, Meditieren, Trainieren und mehr.
Hören Sie sich das gruselige Geräusch eines schwarzen Lochs 250 Millionen Lichtjahre von der Erde entfernt an, angekündigt von der NASA
Schallwellen können sich im Vakuum nicht ausbreiten, daher kann es im Weltraum keinen Schall geben. Die Wissenschaft kann uns jedoch auf vielfältige Weise helfen, das Universum zu hören.