Formel zur Berechnung der Oberfläche und des Volumens einer Kugel

Lassen Sie uns im folgenden Artikel mit Quantrimang.com die Formel zum Berechnen der Oberfläche und des Volumens einer Kugel lernen und überprüfen.

Inhaltsverzeichnis

• Was ist eine Kugel?
  • Was ist eine Kugel?
• Formel zur Berechnung der Oberfläche und des Volumens einer Kugel
  • Formel zur Berechnung der Kugeloberfläche
  • Formel zur Berechnung des Volumens einer Kugel:
• Formel zur Berechnung des Kugelradius
  • Die Seite der Kugel, die die Pyramide umschreibt, steht senkrecht zur Basis.
  • Quadratisches Tetraeder (dies ist ein Sonderfall der Formel 1)
  • Ein vertikales Prisma hat eine Basis, die ein einbeschriebenes Polygon ist.
  • Formel für ein Tetraeder, dessen Eckpunkte die Eckpunkte eines geraden Prismas sind
  • Formel zur Berechnung des Kugelradius einer Pyramide mit senkrecht zur Grundfläche stehenden Seitenflächen
• Beispiele zur Berechnung von Oberfläche und Volumen einer Kugel

Was ist eine Kugel?

Eine Kugelr ist der Ort von Punkten, die im dreidimensionalen Raum von einem gegebenen Fixpunkt O gleich weit entfernt sind . Der Punkt O wird als Mittelpunkt bezeichnet, die Entfernung rals Radius der Kugel.

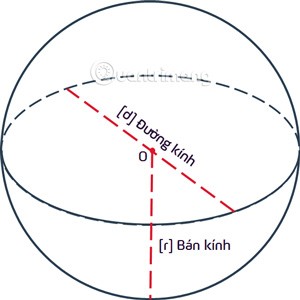
Was ist eine Kugel?

Eine Kugel ist eine Menge von Punkten, die innerhalb einer Kugel liegen, und eine Kugel wird als Kugel oder Kugel mit Mittelpunkt O und Radius r = OA bezeichnet.

Formel zur Berechnung der Oberfläche und des Volumens einer Kugel

Formel zur Berechnung der Kugeloberfläche

Die Oberfläche einer Kugel ist viermal so groß wie die Fläche eines großen Kreises, die wiederum viermal so groß ist wie die Konstante Pi multipliziert mit dem Quadrat des Kugelradius.

Formel zur Berechnung des Volumens einer Kugel:

Das Volumen einer Kugel, auch als Kugelvolumen bekannt, wird berechnet, indem drei Viertel von Pi mit der dritten Potenz des Kugelradius multipliziert werden.

Darin:

• Sist die Oberfläche der Kugel
• Vist das Volumen einer Kugel
• rist der Radius der Kugel/Kugel
• dist eine Kugel/Kugel

Formel zur Berechnung des Kugelradius

Die Seite der Kugel, die die Pyramide umschreibt, steht senkrecht zur Basis.

• Rd ist der Radius der Basis.
• h ist die Länge der Seite senkrecht zur Basis.

Beispiel : Gegeben sei die Pyramide S.ABCD mit rechteckiger Grundfläche, wobei AB = 3a, BC = 4a, SA = 12a und SA senkrecht zur Grundfläche steht. Berechnen Sie den Radius R der Kugel, die die Pyramide S.ABCD umschreibt.

Lösung: Wir haben

Also

Quadratisches Tetraeder (dies ist ein Sonderfall der Formel 1)

Der quadratische Block OABC hat OA, OB, OC, senkrecht zueinander und hat:

Zum Beispiel:

Das Tetraeder OABC hat die senkrecht zueinander stehenden Punkte OA, OB und OC und hat einen Radius von . Das größte Volumen des Tetraeders OABC

Lösung : Wir haben

Auf der anderen Seite haben wir:

Gemäß der AM-GM-Ungleichung haben wir:

Ein vertikales Prisma hat eine Basis, die ein einbeschriebenes Polygon ist.

Darin:

• Rd ist der Radius der Basis
• h ist die Länge der Seite.

Beispiel 1: Gegeben sei eine Kugel mit Radius R, die einen Würfel mit der Seitenlänge a umschreibt. Welche der folgenden Aussagen ist richtig?

A.

B.

C.

D.

Lösung: Wir haben

Die Antwort ist also C.

Formel für ein Tetraeder, dessen Eckpunkte die Eckpunkte eines geraden Prismas sind

Das Tetraeder (H1) hat Eckpunkte, die die Eckpunkte des vertikalen Prismas (H2) sind. Dann gilt:

Formel zur Berechnung des Kugelradius einer Pyramide mit senkrecht zur Grundfläche stehenden Seitenflächen

Dabei sind R und d der Radius der Basis; a und x sind jeweils die Länge des Schnittpunkts zwischen Seitenfläche und Basis und der Winkel an der Oberseite der Seitenfläche, wenn man auf die Basis hinunterblickt.

Oder Sie können die Formel verwenden

Dabei ist Rb der umschriebene Radius der Seitenfläche und a die Länge des Schnittpunkts zwischen Seitenfläche und Basis.

Zum Beispiel: 

Gegeben sei die Pyramide S.ABCD mit quadratischer Grundfläche und das gleichseitige Dreieck SAD mit der Seitenlänge √2a, das in einer Ebene senkrecht zur Grundfläche liegt. Berechnen Sie den Radius R der Kugel, die die Pyramide S.ABCD umschreibt.

A.

B.

Lösung: Wir haben

Die richtige Antwort ist also B.

Beispiele zur Berechnung von Oberfläche und Volumen einer Kugel

Übung 1 : Gegeben sei ein Kreis mit einem Umfang von 31,4 cm. Berechnen Sie das Volumen einer Kugel mit einem Radius, der dem Radius des gegebenen Kreises entspricht.

Preis:

Kreisumfang C = 2πr = 31,4 cm

=> Radius r = C/2π = 5 cm

Das Volumen der gegebenen Kugel beträgt:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 cm³

Lektion 2 : Berechnen Sie das Volumen einer Kugel mit Durchmesser d = 4 cm.

Preis:

Radius r = d/2 = 2 cm

Das Volumen der Kugel beträgt:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 cm³

Lektion 3 :

Lassen Sie einen Kreis mit Durchmesser 4a um seinen Durchmesser rotieren. Wie groß ist das Volumen des rotierenden Festkörpers?

Lösung: Gegeben sei ein Kreis mit Durchmesser 4a, der sich um seinen Durchmesser dreht. So erhalten wir eine Kugel mit Durchmesser 4a bzw. Radius R = 2a.

Das Volumen der Kugel beträgt:

Lektion 4 :

Die Kugel mit Radius R√3 hat eine Fläche von:

A. 4√3πR2

B. 4πR2

C. 6πR2

D. 12πR2

Lösung: Wenden Sie die Formel an: S = 4πR2

Die Oberfläche einer Kugel mit Radius R√3 beträgt: S = 4π(R√3)2 = 12πR2

Die Antwort ist also D.

Zwei kurze Formeln, die man sich aber auf Dauer nur schwer merken kann. Setzen Sie ein Lesezeichen für den Artikel und öffnen Sie ihn bei Bedarf. Ich hoffe, der Artikel ist hilfreich für Sie.

Zusätzlich zu der Formel zur Berechnung der Oberfläche und des Volumens einer Kugel oben können Sie auch die Formel zur Berechnung der Fläche einiger anderer Grundformen wie Dreiecke , Rechtecke , Parallelogramme usw. zu Rate ziehen .