Formel zur Berechnung der Mantelfläche eines Kegelstumpfes, der Gesamtfläche eines Kegelstumpfes, des Volumens eines Kegelstumpfes

Wir laden Sie ein, im folgenden Artikel zu erfahren, was ein Kegelstumpf ist, die Formel zur Berechnung des Volumens eines Kegelstumpfes, die Mantelfläche und die Gesamtfläche eines Kegelstumpfes.

Wie Sie aus dem vorherigen Artikel erfahren haben, entsteht eine Pyramide , wenn ein rechtwinkliges Dreieck eine Umdrehung um seine Achse (eine rechtwinklige Seite) gedreht wird.

Kegelstumpf

• 1. Berechnen Sie die Fläche eines Kegelstumpfes
  • 1.1. Berechnen Sie die Mantelfläche eines Kegelstumpfes
  • 1.2. Berechnen Sie die Gesamtfläche eines Kegelstumpfes
• 2. Berechnen Sie das Volumen eines Kegelstumpfes
• Was ist ein Kegelstumpf?

1. Berechnen Sie die Fläche eines Kegelstumpfes

Die Fläche eines Kegelstumpfes wird oft mit zwei Begriffen bezeichnet: Mantelfläche und Gesamtfläche.

1.1. Berechnen Sie die Mantelfläche eines Kegelstumpfes

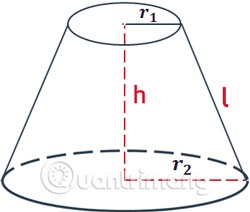
Darin:

• Der Umfang ist die Fläche um den Kegelstumpf.
• r1und r2ist der Radius der beiden Grundflächen des Kegelstumpfes.
• list die Länge der Erzeugenden des Kegelstumpfes.

Die Mantelfläche eines Kegelstumpfes umfasst nur die Fläche der den Kegel umgebenden Flächen, nicht jedoch die Fläche der beiden Grundflächen.

Formel zur Berechnung der Mantelfläche: gleich der Differenz der Mantelflächen des großen Kegels und des kleinen Kegels.

1.2. Berechnen Sie die Gesamtfläche eines Kegelstumpfes

• r1und r2ist der Radius der beiden Grundflächen des Kegelstumpfes.
• list die Länge der Erzeugenden des Kegelstumpfes.

Somit:

Darin:

• Die Fläche um einen Kegelstumpf ist die Fläche um ihn herum.
• Stoalphan ist die Gesamtoberfläche eines Kegelstumpfes.
• S2day ist die Fläche der beiden Bodenflächen

Die Gesamtfläche errechnet sich aus der Größe der gesamten von der Figur eingenommenen Fläche, einschließlich der Mantelfläche und der Fläche der beiden kreisförmigen Grundflächen.

Formel zur Berechnung der Gesamtfläche: entspricht der Seitenfläche plus der Fläche von 2 Grundflächen.

Zum Beispiel:

Gegeben sei ein Kegelstumpf mit Basisradien r1 und r2 von 5 cm bzw. 7 cm. Die Mantellinie, die die Spitze mit der Basis des Kegels verbindet, ist 6 cm lang. Wie groß sind die Gesamtfläche und die Mantelfläche dieses Kegels?

Preis:

Wenn wir die Formel zur Berechnung der Gesamtfläche eines Kegelstumpfes anwenden, erhalten wir r1 = 5 cm, r2 = 7 cm und die Länge der Erzeugenden l = 6 cm. Bestimmen Sie die Gesamtfläche eines Kegelstumpfes, indem Sie die folgende Formel anwenden:

Stp = π.(5 + 7).4 + (π.52 + π.72) = π.12.4 + (π.25 + π.49) = 383,08 (cm2).

Somit beträgt die Gesamtfläche dieses Kegelstumpfes etwa 383,08 cm².

Die Mantelfläche eines Kegelstumpfes beträgt:

Sxq = π.(r1 + r2).l = π.(5 +7).6 ~ 226 cm2.

2. Berechnen Sie das Volumen eines Kegelstumpfes

Das Volumen eines Kegelstumpfs ist die Menge an Raum, die der Kegelstumpf einnimmt.

Formel zur Berechnung des Volumens eines Kegelstumpfes: gleich der Volumendifferenz des großen Kegels und des kleinen Kegels.

Darin:

• Vist das Volumen des Kegelstumpfes.
• r1und r2ist der Radius der beiden Grundflächen des Kegelstumpfes.
• hist die Höhe des Kegelstumpfes (Abstand zwischen den beiden Grundflächen).

Beispiel : Gegeben sei ein Kegelstumpf mit Basisradien r1 und r2 von 5 cm bzw. 9 cm. Die Verbindungshöhe zwischen den beiden Basisradien beträgt 8 cm. Wie groß ist die Gesamtoberfläche dieses Kegels?

Preis: 

Wenn wir die Formel zur Berechnung des Volumens eines Kegelstumpfes anwenden, erhalten wir: r1 = 5 cm, r2 = 9 cm, h = 8 cm.
V = 1/3π.8. (52 + 5,9 +92) = 1264,37 (cm3).

Somit beträgt das Volumen dieses Kegelstumpfes ungefähr 1264,367 cm3.

Beispiel 2:

Gegeben sei ein Kegelstumpf wie in der Abbildung dargestellt.

Da der Radius der kleinen Basis r = 3 cm beträgt, beträgt der Radius der großen Basis R = 6 cm und die Länge AB = 4 cm. Berechnen Sie die Mantelfläche und das Volumen des Kegelstumpfes.

Preis:

Die Mantelfläche eines Kegelstumpfes beträgt:

Sxq = π(r + R)l = π(3 + 6).4 = 36π (cm2)

Zur Berechnung der Höhe eines Kegelstumpfes steht uns folgende Zeichnung zur Verfügung:

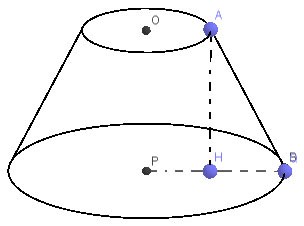
Wenn wir den Satz des Pythagoras und das rechtwinklige Dreieck AHB bei H anwenden, erhalten wir:

Das Volumen eines Kegelstumpfes beträgt:

• Formel zur Berechnung des Volumens eines Pyramidenstumpfes, der Mantelfläche und der Gesamtfläche eines Pyramidenstumpfes

Was ist ein Kegelstumpf?

Wenn ein Kegel von einer Ebene geschnitten wird, die parallel zur Basis ist, ist der Teil der Ebene innerhalb des Kegels ein Kreis . Der Teil der Form zwischen der oberen Ebene und der Basis wird als Kegelstumpf bezeichnet.

Man kann sich vorstellen, dass ein Kegelstumpf eine Form mit zwei Grundflächen ist, die zwei Kreise mit unterschiedlichen Radien sind, die auf zwei parallelen Ebenen liegen, wobei die Linie, die die Mittelpunkte verbindet, die Symmetrieachse ist.

Sie können leicht erkennen, dass uns im Leben häufig Kegelstümpfe begegnen, beispielsweise bei Eimern oder Lampenschirmen. Hoffentlich haben Sie durch den obigen Artikel ein besseres Verständnis von Kegelstümpfen und davon, wie man die Fläche und das Volumen von Kegelstümpfen berechnet.