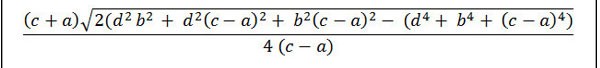Formel zur Berechnung der Fläche eines Trapezes: regelmäßig, quadratisch, gleichschenklig

Ein Trapez ist ein konvexes Viereck mit zwei parallelen Seiten, den sogenannten Grundflächen, und den übrigen Seiten, den sogenannten Lateralflächen. Die Formel zur Berechnung des Umfangs und der Fläche eines Trapezes gehört zu den grundlegenden mathematischen Kenntnissen, die sowohl im Studium als auch im Alltag häufig angewendet werden. Der folgende Artikel stellt Ihnen die Formel zur Berechnung der Fläche und der Länge der Grundfläche eines Trapezes vor. Bitte beachten Sie ihn.

Inhaltsverzeichnis

• Formel zur Berechnung der Fläche eines Trapezes
  • Formel zur Berechnung der Fläche eines Trapezes bei Kenntnis von 4 Seiten (fortgeschrittenes Problem)
• So berechnen Sie die Fläche eines quadratischen Trapezes
• So berechnen Sie die Fläche eines gleichschenkligen Trapezes
• Berechnen Sie die Länge der Basis des Trapezes
• Arten der Mathematik zur Berechnung der Fläche eines Trapezes

Formel zur Berechnung der Fläche eines Trapezes

Es gibt ein Trapez ABCD mit der Basis AB, der Länge a, der Basis CD, der Länge b und der Höhe h.

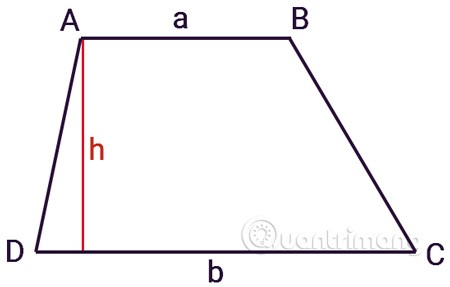
Die Fläche eines Trapezes ist gleich dem Durchschnitt der beiden Grundflächen multipliziert mit der Höhe zwischen den beiden Grundflächen.

Darin:

• S ist die Fläche des Trapezes.
• a und b sind die Längen der beiden Basiskanten.
• h ist die Höhe von der Basiskante a bis b oder umgekehrt (Abstand zwischen 2 Basiskanten).

Es gibt auch ein Gedicht über die Berechnung der Fläche eines Trapezes, das man sich ganz einfach wie folgt merken kann:

Möchten Sie die Fläche eines Trapezes berechnen

Wir addieren den großen Boden und den kleinen Boden.

Addieren und mit der Höhe multiplizieren

Halbieren und zur Hälfte entnehmen, es kommt trotzdem raus.

Formel zur Berechnung der Fläche eines Trapezes bei Kenntnis von 4 Seiten (fortgeschrittenes Problem)

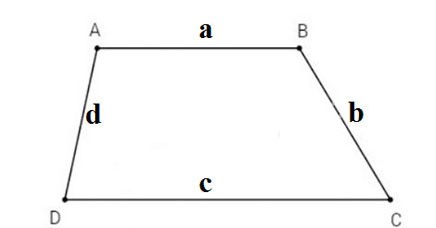
Falls in der Aufgabe Angaben zur Länge von 4 Seiten gemacht werden und die Basisseiten a und c klar angegeben sind, wobei Basisseite c größer als Basisseite a ist und die Seiten b und d sind, können Sie die Fläche des Trapezes mit der folgenden Formel berechnen.

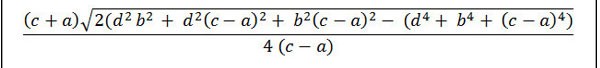
Darin:

• S: Fläche
• a: kleine Basis
• c: große Basiskante
• b, d: Seiten des Trapezes

So berechnen Sie die Fläche eines quadratischen Trapezes

Ein rechtwinkliges Trapez ist ein Trapez mit einem rechten Winkel. Die senkrecht zu den beiden Grundflächen stehende Seite ist gleichzeitig die Höhe h des Trapezes.

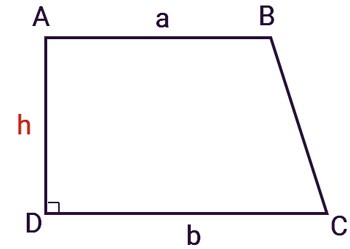
Die allgemeine Formel zur Berechnung der Fläche eines geraden Trapezes ähnelt der eines regelmäßigen Trapezes: der Durchschnitt der beiden Basisseiten multipliziert mit der Höhe zwischen den beiden Basisseiten , jedoch ist die Höhe hier die Seite, die senkrecht zu beiden Basisseiten steht.

Darin:

• S ist die Fläche des Trapezes.
• a und b sind die Längen der beiden Basiskanten.
• h ist die Länge der Seite, die senkrecht zu den beiden Grundflächen steht.

So berechnen Sie die Fläche eines gleichschenkligen Trapezes

Ein gleichschenkliges Trapez ist ein Trapez, dessen zwei benachbarte Winkel gleich groß sind. Die beiden Seiten eines gleichschenkligen Trapezes sind gleich groß und nicht parallel.

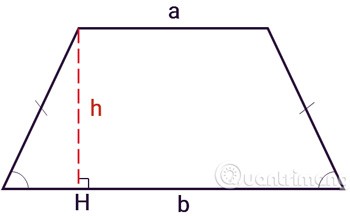
Neben der üblichen Anwendung der Formel zur Berechnung eines Trapezes können Sie das gleichschenklige Trapez auch in kleinere Teile zerlegen, die Flächeninhalte der einzelnen Teile berechnen und diese anschließend addieren.

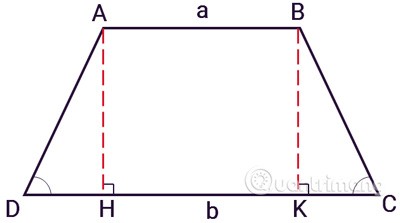
Beispielsweise hat das gleichschenklige Trapez ABCD zwei gleich lange Seiten: AD und BC. Mit den Höhen AH und BK wird das Trapez in ein Rechteck ABKH und zwei Dreiecke ADH und BCK unterteilt. Wenden Sie die Formel zur Berechnung der Rechteckfläche für ABHK und der Dreieckfläche für ADH und BCK an und addieren Sie anschließend alle Flächen, um die Fläche des Trapezes ABCD zu ermitteln.

Konkret so:

Und SADH = SBCK (leicht zu beweisen), erhalten wir:

Berechnen Sie die Länge der Basis des Trapezes

Wenn Sie die Fläche, Höhe und Länge einer Seite der Basis kennen, können Sie die Länge der verbleibenden Seite wie folgt berechnen:

Arten der Mathematik zur Berechnung der Fläche eines Trapezes

Beispiel 1: Berechnen Sie die Fläche eines Trapezes

Berechnen Sie die Fläche eines Trapezes, wobei Sie wissen, dass die Länge der beiden Basen 18 cm bzw. 14 cm beträgt. Die Höhe beträgt 9 cm

Preis: 

Wenn wir die Formel zur Berechnung der Fläche eines Trapezes anwenden, erhalten wir:

Die Fläche des Trapezes beträgt also 144cm2

Beispiel 2: 

Es gibt ein trapezförmiges Grundstück mit einer kleinen Grundfläche von 24 m und einer großen Grundfläche von 30 m. Erweitern Sie die beiden Grundflächen rechts vom Grundstück, indem Sie die große Grundfläche um 7 m und die kleine Grundfläche um 5 m erweitern. So erhalten Sie ein neues trapezförmiges Grundstück mit einer Fläche, die 36 m² größer ist als die ursprüngliche Fläche. Berechnen Sie die Fläche des ursprünglichen trapezförmigen Grundstücks.

Preis:

Gemäß der Aufgabe ist die vergrößerte Fläche die Fläche eines Trapezes mit einer großen Basis von 7 m und einer kleinen Basis von 5 m. Daher beträgt die Höhe des trapezförmigen Grundstücks: h = (36 x 2) : (7 + 5) = 6 m

Die ursprüngliche Fläche des Grundstücks beträgt: S = 6 . (24 + 30) : 2 = 162m²

Lektion 3:

Bei einem quadratischen Trapez mit einem Abstand von 16 cm zwischen den beiden Basisflächen beträgt die kleine Basis ¾ der großen Basisfläche. Berechnen Sie die Länge der beiden Basisflächen, wenn Sie wissen, dass die Fläche des quadratischen Trapezes 112 cm² beträgt.

Preis:

Der Abstand zwischen den beiden Grundflächen eines geraden Trapezes ist die Höhe des Trapezes, also:

Die Gesamtlänge der beiden Basen beträgt (112 x 2) : 16 = 14cm

Wir nennen die Länge der kleinen Basis a, die Länge der großen Basis b, wir haben:

a + b = 14 und a = ¾ b

Also a = 14 x 4: 7 = 8 cm

Daher kleine Basis = 34/7 cm, große Basis = 64/7 cm

Beispiel 4: Gleichschenkliges Trapez ABCD (AB//CD) hat AB = 5 cm, CD = 13 cm, AD = 5 cm. Berechnen Sie die Fläche des Trapezes ABCD?

Preis:

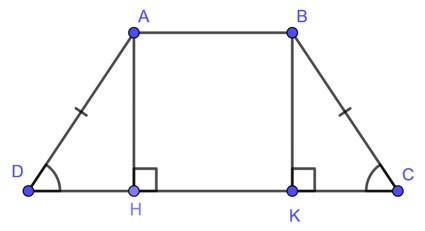
Seien AH und BK die beiden Höhen des Trapezes. Dann ist ABKH ein Rechteck, wir haben:

Wenn wir den Satz des Pythagoras auf das rechtwinklige Dreieck AHD anwenden, erhalten wir:

Also: AH = 3cm

Die Fläche des Trapezes ABCD beträgt also:

Oben finden Sie einen Artikel von Quantrimang.com über die gängigste Formel und Methode zur Berechnung der Fläche eines Trapezes. Ich hoffe, der Artikel ist hilfreich für Sie!