Formel zur Berechnung der Fläche eines Dreiecks: rechtwinklig, regelmäßig, gleichschenklig, gleichseitig

Wie lautet die Formel zur Berechnung der Fläche eines regelmäßigen, rechtwinkligen und gleichschenkligen Dreiecks ? Im folgenden Artikel erfahren Sie mehr über die einfachsten und am häufigsten verwendeten Methoden zur Berechnung der Fläche eines Dreiecks.

Inhaltsverzeichnis

• 1. Berechnen Sie die Fläche eines regelmäßigen Dreiecks
• 2. Berechnen Sie die Fläche eines gleichschenkligen Dreiecks
• 3. Berechnen Sie die Fläche eines gleichseitigen Dreiecks
• 4. Berechnen Sie die Fläche eines rechtwinkligen Dreiecks
• 5. Berechnen Sie die Fläche eines rechtwinkligen gleichschenkligen Dreiecks
• 6. Formel zur Berechnung der Fläche eines Dreiecks im Oxyz-Koordinatensystem
• Arten von Dreiecken

1. Berechnen Sie die Fläche eines regelmäßigen Dreiecks

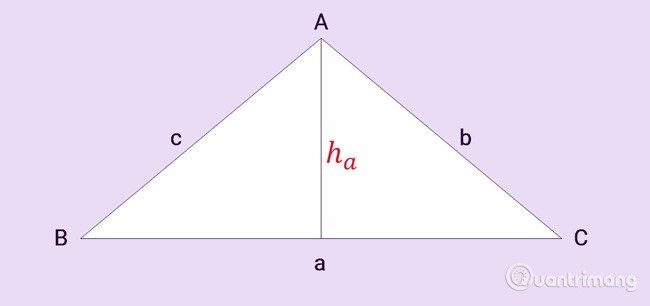
Das Dreieck ABC hat drei Seiten a, b, c, ha ist die Höhe vom Scheitelpunkt A, wie gezeigt:

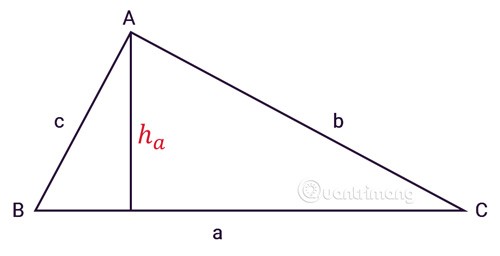
a. Allgemeine Formel

Die Fläche eines Dreiecks ist gleich der Höhe multipliziert mit der Länge der gegenüberliegenden Seite (der Basis) und geteilt durch 2.

Gedicht zur Berechnung der Fläche eines regelmäßigen Dreiecks

Die Fläche eines Dreiecks lässt sich einfach berechnen.
Multipliziere die Höhe mit der Basis und dividiere das Ergebnis in zwei Hälften.

Zum Beispiel:

Berechnen Sie die Fläche eines Dreiecks mit einer Basislänge von 5m und einer Höhe von 24dm.

Lösung: Höhe 24dm = 2,4m

Die Fläche des Dreiecks beträgt:

b. Berechnen Sie die Fläche eines Dreiecks, wenn Sie einen Winkel kennen

Die Fläche eines Dreiecks ist gleich der Hälfte des Produkts zweier benachbarter Seiten mal dem Sinus des Winkels zwischen diesen beiden Seiten im Dreieck.

Zum Beispiel:

Dreieck ABC hat Seite BC = 7, Seite AB = 5, Winkel B beträgt 60 Grad. Berechnen Sie die Fläche des Dreiecks ABC?

Preis:

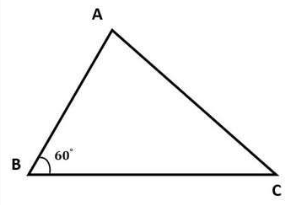
c. Berechnen Sie die Fläche eines Dreiecks, wenn Sie 3 Seiten kennen, mithilfe der Heron-Formel.

Mit der bewährten Heron-Formel:

Wobei p der Halbumfang des Dreiecks ist:

Kann mit der Formel umgeschrieben werden:

Zum Beispiel:

Berechnen Sie die Fläche des Dreiecks mit den Seitenlängen AB = 8, AC = 7, CB = 9

Preis:

Der Halbumfang des Dreiecks ABC beträgt

Wenn wir die Heldenformel anwenden, haben wir

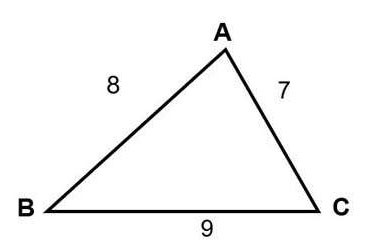
d. Berechnen Sie die Fläche mithilfe des Radius des Kreises, der das Dreieck umschreibt (R).

Andere:

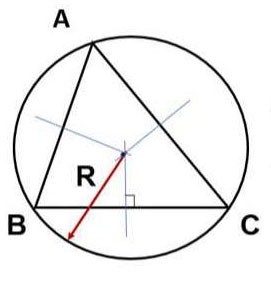
Hinweis: Es muss bewiesen werden, dass R der Radius des Kreises ist, der das Dreieck umschreibt.

Zum Beispiel:

Gegeben sei das Dreieck ABC. Die Seitenlängen betragen a = 6, b = 7, c = 5, R = 3 (R ist der Radius des Kreises, der das Dreieck ABC umschreibt). Berechnen Sie die Fläche des Dreiecks ABC.

Preis:

e. Berechnen Sie die Fläche mithilfe des Radius des in das Dreieck eingeschriebenen Kreises (r).

• p: Halber Umfang des Dreiecks.
• r: Radius des eingeschriebenen Kreises.

Beispiel: Berechnen Sie die Fläche des Dreiecks ABC, wenn Sie die Längen der Seiten kennen: AB = 20, AC = 21, BC = 15, r = 5 (r ist der Radius des Kreises, der in das Dreieck ABC einbeschrieben ist).

Preis:

Der Halbumfang eines Dreiecks beträgt:

r= 5

Die Fläche des Dreiecks beträgt:

2. Berechnen Sie die Fläche eines gleichschenkligen Dreiecks

Gleichschenklige Dreiecke ähneln regelmäßigen Dreiecken. Wir können die Formel anwenden, indem wir die Höhe mit der Grundlinie multiplizieren und dann wie oben beschrieben durch 2 dividieren. Darüber hinaus gibt es komplexere Formeln:

Das gleichschenklige Dreieck ABC hat drei Seiten, a ist die Länge der Basis, b ist die Länge der beiden Seiten und ha ist die Höhe vom Scheitelpunkt A, wie gezeigt:

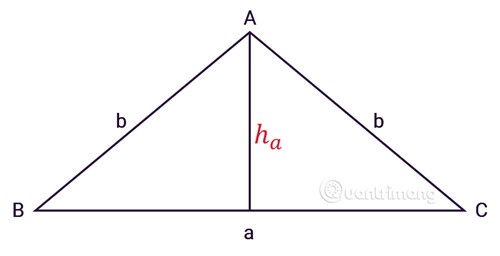
Wenn wir die Formel zur Berechnung der Fläche eines regelmäßigen Dreiecks anwenden, erhalten wir die Formel zur Berechnung der Fläche eines gleichschenkligen Dreiecks:

3. Berechnen Sie die Fläche eines gleichseitigen Dreiecks

Das gleichseitige Dreieck ABC hat drei gleich lange Seiten, a ist die Länge der Seiten, wie gezeigt:

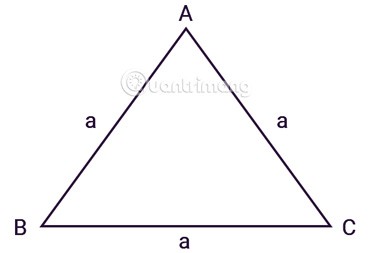
Wenn wir den Satz von Heron anwenden, um dies abzuleiten, erhalten wir die Formel zur Berechnung der Fläche eines gleichseitigen Dreiecks:

4. Berechnen Sie die Fläche eines rechtwinkligen Dreiecks

Das Dreieck ABC hat an der Stelle B einen rechten Winkel, a, b sind die Längen der beiden rechtwinkligen Seiten:

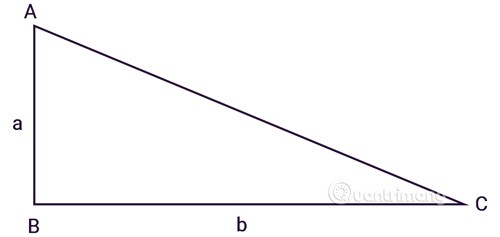
Wenden Sie die Formel zur Berechnung der Fläche eines rechtwinkligen Dreiecks an, wobei die Höhe eine der beiden Seiten des rechten Winkels und die Basis die verbleibende Seite ist.

Formel zur Berechnung der Fläche eines rechtwinkligen Dreiecks:

Gedicht zur Berechnung der Fläche eines rechtwinkligen Dreiecks:

Dreieck mit zwei rechten Winkeln.
Bleiben Sie ruhig, geraten Sie nicht in Panik und machen Sie keine Fehler.

Seite, Seite multipliziert, geteilt durch zwei
ist die Fläche, machen Sie die Übung schnell

5. Berechnen Sie die Fläche eines rechtwinkligen gleichschenkligen Dreiecks

Das Dreieck ABC ist ein rechtwinkliges Dreieck bei A, a ist die Länge der beiden Seiten:

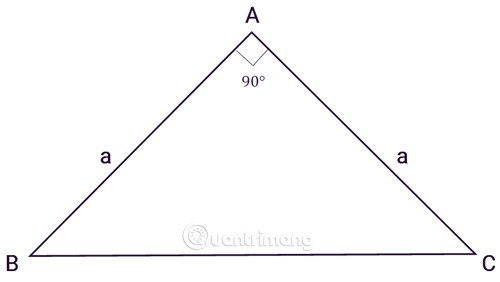
Wenn wir die Formel zur Berechnung der Fläche eines rechtwinkligen Dreiecks auf die Fläche eines gleichschenkligen rechtwinkligen Dreiecks mit gleicher Höhe und Basis anwenden, erhalten wir die Formel:

6. Formel zur Berechnung der Fläche eines Dreiecks im Oxyz-Koordinatensystem

Theoretisch können wir die obigen Formeln verwenden, um die Fläche eines Dreiecks im Raum oder im Oxyz-Raum zu berechnen. Dies ist jedoch mit einigen Berechnungsschwierigkeiten verbunden. Daher wird die Fläche eines Dreiecks im Oxyz-Raum häufig mithilfe des Richtungsprodukts berechnet.

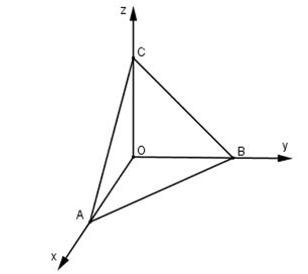
Im Raum Oxyz ist das Dreieck ABC gegeben. Die Fläche des Dreiecks ABC berechnet sich nach der Formel:

Beispiel :

Im Oxyz-Raum ist ein Dreieck ABC mit den Koordinaten der drei Eckpunkte A(-1;1;2), B(1;2;3), C(3;-2;0) gegeben. Berechnen Sie die Fläche des Dreiecks ABC.

Lösung :

Wir haben:

Um die Fläche eines Dreiecks zu berechnen, müssen Sie feststellen, um welche Art von Dreieck es sich handelt. Von dort aus finden Sie die richtige Formel zur Flächenberechnung und die erforderlichen Faktoren, um die Fläche eines Dreiecks so schnell wie möglich zu berechnen.

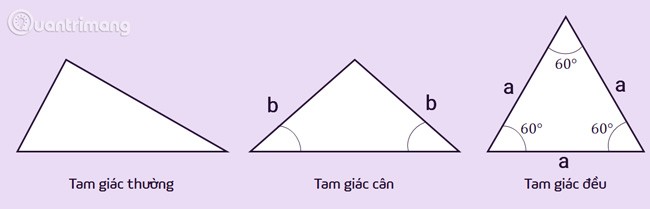
Arten von Dreiecken

Regelmäßiges Dreieck: ist das einfachste Dreieck mit unterschiedlichen Seitenlängen und unterschiedlichen Innenwinkelmaßen. Regelmäßige Dreiecke können auch Sonderformen von Dreiecken umfassen.

Gleichschenkliges Dreieck: ist ein Dreieck mit zwei gleich langen Seiten. Diese beiden Seiten werden als Lateralseiten bezeichnet. Der Scheitelpunkt eines gleichschenkligen Dreiecks ist der Schnittpunkt der beiden Lateralseiten. Der vom Scheitelpunkt gebildete Winkel wird als Scheitelwinkel bezeichnet, die beiden anderen Winkel als Basiswinkel. Die Eigenschaft eines gleichschenkligen Dreiecks ist, dass die beiden Basiswinkel gleich groß sind.

Gleichseitiges Dreieck: ist ein Sonderfall eines gleichschenkligen Dreiecks, bei dem alle drei Seiten gleich lang sind. Die Eigenschaft eines gleichseitigen Dreiecks besteht darin, dass es drei gleich große Winkel hat und 60 Grad beträgt.

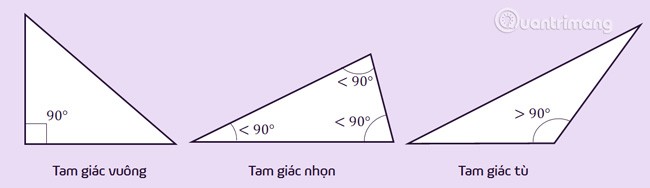
Rechtwinkliges Dreieck: ist ein Dreieck mit einem Winkel von 90 (ein rechter Winkel).

Stumpfes Dreieck: ist ein Dreieck mit einem Innenwinkel größer als 90 (stumpfer Winkel) oder einem Außenwinkel kleiner als 90 (spitzer Winkel).

Spitzwinkliges Dreieck: ist ein Dreieck mit drei Innenwinkeln, die alle kleiner als 90 sind (drei spitze Winkel) oder mit allen Außenwinkeln größer als 90 (sechs stumpfe Winkel).

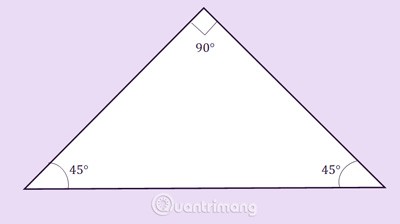
Rechtwinkliges gleichschenkliges Dreieck: ist sowohl ein rechtwinkliges als auch ein gleichschenkliges Dreieck.

• Formel zur Berechnung des Umfangs eines Dreiecks
• Formel zur Berechnung der Höhe in regelmäßigen, gleichschenkligen, gleichseitigen und rechtwinkligen Dreiecken
• Was ist der Schwerpunkt? Formel zur Berechnung des Schwerpunkts eines Dreiecks
• Was ist eine Mittelsenkrechte?

Oben finden Sie eine Zusammenfassung gängiger Formeln zur Berechnung der Dreiecksfläche im Oxyz-Koordinatensystem. Bei Fragen, Anmerkungen oder Anregungen hinterlassen Sie bitte unten einen Kommentar, um ihn mit Quantrimang.com zu besprechen.