Formel zur Berechnung der Fläche einer Raute, des Umfangs einer Raute

Lassen Sie uns im folgenden Artikel die Formel zur Berechnung der Fläche, des Umfangs und der Diagonale einer Raute wiederholen und auswendig lernen.

Inhaltsverzeichnis

• 1. Formel zur Berechnung der Fläche einer Raute
  • Formel zur Berechnung der Fläche einer Raute basierend auf Basis und Höhe
  • Formel zur Berechnung der Fläche einer Raute basierend auf der Dreiecksformel (Wenn Sie den Winkel der Raute kennen)
• 2. Formel zur Berechnung des Umfangs einer Raute
• 3. Was ist eine Raute?
  • Eigenschaften der Raute
• 4. Beispiel zur Berechnung von Fläche und Umfang einer Raute

1. Formel zur Berechnung der Fläche einer Raute

Die Fläche einer Raute wird anhand der Größe der Oberfläche gemessen, also des sichtbaren flachen Teils der Raute.

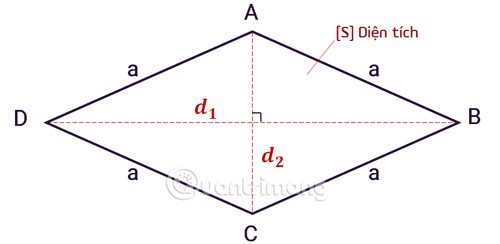
Formel zur Berechnung der Fläche einer Raute basierend auf Basis und Höhe

Die Fläche einer Raute ist gleich dem halben Produkt der Längen der beiden Diagonalen , die Formel lautet wie folgt:

Darin:

• Sist die Fläche der Raute.
• d1und d2sind die beiden Diagonalen einer Raute.

Beispiel zur Berechnung der Fläche einer Raute.

Lektion 1: Es gibt ein rautenförmiges Stück Pappe mit zwei sich kreuzenden Diagonalen von 6 cm bzw. 8 cm Länge. Wie groß ist die Fläche des rautenförmigen Stücks Pappe?

Wenn wir die Methode zur Berechnung der Fläche einer Raute anwenden, erhalten wir d1 = 6 cm und d2 = 8 cm. Wir setzen es in die Formel ein und erhalten das folgende Ergebnis:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Formel zur Berechnung der Fläche einer Raute basierend auf der Dreiecksformel (Wenn Sie den Winkel der Raute kennen)

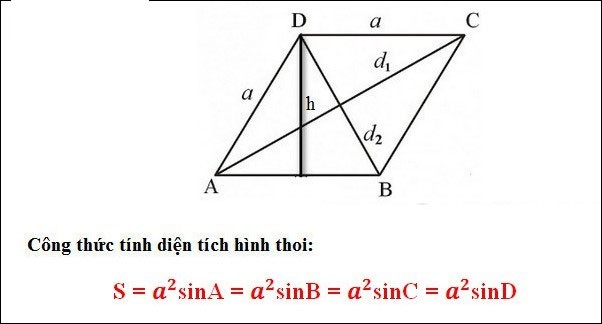
Dabei gilt: a: Seite der Raute

Beispiel 1 : Gegeben sei eine Raute ABCD mit Rautenkante = 4 cm, Winkel A = 35 Grad. Berechnen Sie die Fläche der Raute ABCD.

Lösung: Mit der Formel erhalten wir a = 4, Winkel = 35 Grad. Wir setzen Folgendes in die Formel ein:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

2. Formel zur Berechnung des Umfangs einer Raute

Der Umfang einer Raute wird berechnet, indem die Längen der Linien addiert werden, die die Form umgeben. Dies ist auch die Linie, die die gesamte Fläche umgibt.

Um den Umfang einer Raute zu berechnen, berechnen wir die Summe der Längen der vier Seiten. Die genaue Formel lautet wie folgt:

Darin:

• Pist der Umfang einer Raute.
• aist die Länge der Seite der Raute.

Beispiel: Gegeben sei eine Raute ABCD mit gleicher Seitenlänge und 7 cm. Wie groß ist der Umfang dieser Raute?

Gemäß der oben vorgestellten Formel zur Berechnung des Umfangs einer Raute ergibt sich a = 7 cm. Der Umfang der Raute ABCD berechnet sich somit wie folgt:

P (ABCD) = ax 4 = 7 x 4 = 28 cm

3. Was ist eine Raute?

Eine Raute ist ein Viereck mit vier gleich langen Seiten. Es ist ein Parallelogramm mit zwei gleich langen benachbarten Seiten oder ein Parallelogramm mit zwei senkrecht aufeinander stehenden Diagonalen.

Eigenschaften der Raute

• 2 gleich große, gegenüberliegende Winkel
• 2 Diagonalen stehen senkrecht zueinander und schneiden sich im Mittelpunkt jeder Linie
• Die beiden Diagonalen sind die Winkelhalbierenden.

In diesem Artikel stellt Quantrimang.com für Ihr Studium und Ihre Arbeit erneut effektive Formeln zur Berechnung der Fläche und des Umfangs einer Raute vor.

4. Beispiel zur Berechnung von Fläche und Umfang einer Raute

Beispiel 1: 

Gegeben sei eine Raute ABCD mit einer Seitenlänge AD = 4 m und einem Winkel DAB = 30 Grad. Berechnen Sie die Fläche der Raute ABCD.

Preis:

Da ABCD eine Raute ist, sind die gebildeten Dreiecke gleichschenklig. Sei I der Mittelpunkt der beiden Diagonalen, sodass AI senkrecht auf BD steht und der Winkel IAB 15 Grad beträgt.

Daher ist AI = AB. cos IAB = 4. Cos 15 = 3,84 m.

Betrachten wir das rechtwinklige Dreieck ABI. Nach dem Satz des Pythagoras gilt:

BI2 = AB2 - AI2 = 1,25 m

Also BI = 1,1 m

AC = 2. AI = 7,68 m

BD = 2. BI = 2,2 m

Basierend auf der Formel zur Berechnung der Fläche einer Raute haben wir die Fläche einer Raute ABCD = ½ . AC . BD = 8,45(m2)

Beispiel 2: Gegeben sei eine Raute mit einer Seitenlänge von 6 cm und einem Winkel von 60°. Berechnen Sie die Fläche der Raute.

Mit diesen Fakten fehlt dir die Grundlage, um die Fläche einer Raute zu berechnen. Du musst dich auf die Eigenschaften von Rauten, die Eigenschaften gleichseitiger Dreiecke und die Berechnung der Seiten in einem rechtwinkligen Dreieck verlassen, um die Diagonale der Raute zu berechnen. Die Schritte sind wie folgt:

Schritt 1: Zeichnen Sie ein Bild und notieren Sie die bekannten Fakten.

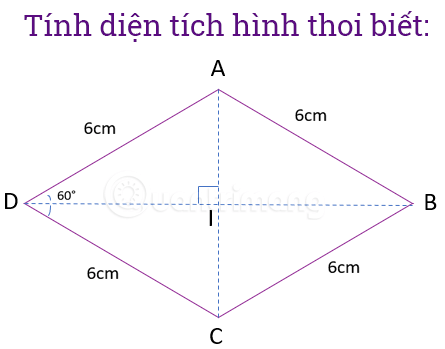
Schritt 2: Wenn wir die Eigenschaften einer Raute anwenden, erhalten wir:

Die Diagonale AC ist die Winkelhalbierende von Winkel A, daher ist der Winkel gleich 1/2 Winkel und 60°. (Die Summe der Innenwinkel eines Vierecks beträgt 360°, die Summe der Innenwinkel eines Dreiecks 180°). Somit ist das Dreieck ADC ein gleichseitiges Dreieck => Seite AC ist 6 cm lang. I ist der Mittelpunkt von AC => AI=3 cm.

Schritt 3: Berechnen Sie die Länge von DI

Das Dreieck DIA ist an der Stelle I rechtwinklig, die Seite DI wird wie folgt berechnet:

=> cm

Schritt 4: Berechnen Sie die Fläche der Raute ABCD:

Beispiel 3: Bei einer Raute ABCD mit einer Seitenlänge von 13 cm schneiden sich zwei Diagonalen bei H.

Berechnen Sie die Fläche der Raute ABCD, wobei Sie wissen, dass BH eineinhalb mal AH ist.

Lösung:

ABCD ist eine Raute, also ist AH senkrecht zu BH bei H, dann ist das Dreieck ABH bei H rechtwinklig.

Sei BH = 2a, dann ist AH = 3a.

Nach dem Satz des Pythagoras gilt: AH²+ BH²= AB² ⇒9a²+4a²=13 ⇒13a²=13 ⇒a=1

Daher AH= 3cm, BH= 2cm oder AC= 6cm, BD= 4cm

Die Fläche der Raute beträgt: S = 6,4/2= 12cm².

Beispiel 4 :

Gegeben sei die Raute MNPQ, Winkel A = 30°, Umfang = 20 m, Mittelpunkt der Diagonale ist I. Wie groß ist die Fläche der Raute MNPQ?

Lösung

Die Seitenlänge der Raute beträgt a = P : 4 = 20 : 4 = 5m

Da die durch Rauten gebildeten Dreiecke alle gleichschenklige Dreiecke sind, wird das Dreieck, das aus dem Mittelpunkt der Diagonale I, den Punkten M und N gebildet wird, durch den Winkel IMN = 15° gebildet.

Länge der halben Diagonale MI = MN x cos IMN = 5 x cos150 = 4,8 m

Wenn wir den Satz des Pythagoras im rechtwinkligen Dreieck MNI anwenden, erhalten wir: NI = 1,4m

Diagonale Länge NQ = 2 x NI = 2 x 1,4 = 2,8m

Die Fläche der Raute MNPQ beträgt S = 2 x ½ x NQ x MI = 1 x ½ x 2,8 x 4,8 = 13,44 m²

Antwort: 13,44 m²

Wenn Sie Fragen zur Formel zur Berechnung von Fläche und Umfang einer Raute haben, hinterlassen Sie bitte unten einen Kommentar, um gemeinsam zu diskutieren und zu beantworten. Vielen Dank, dass Sie den Artikel verfolgt haben.