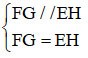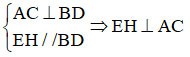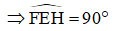Wie man die Diagonale eines Quadrats berechnet, wie man die Diagonale eines Rechtecks berechnet, wird häufig in mathematischen Problemen und praktischen Anwendungen wie Design und Konstruktion, Ecken abschneiden, Messen usw. verwendet. Quantrimang.com hat Wissen über die Eigenschaften zweier Diagonalen sowie Berechnungsformeln zusammengestellt, die Sie zur Anwendung in Studium, Leben und Beruf heranziehen können.
Inhaltsverzeichnis
Wie groß ist die Diagonale eines Quadrats und eines Rechtecks?
Die Diagonale eines Quadrats oder Rechtecks ist eine gerade Linie, die zwei gegenüberliegende Ecken verbindet. Jedes Quadrat oder Rechteck hat zwei gleich lange Diagonalen.
So berechnen Sie die Diagonale eines Quadrats
Eigenschaften der quadratischen Diagonale
- Die beiden Diagonalen eines Quadrats sind gleich lang, senkrecht zueinander und schneiden sich jeweils in der Mitte.
- Es gibt einen Inkreis und einen Umkreis, und die Mittelpunkte beider Kreise fallen zusammen und sind die Schnittpunkte der beiden Diagonalen des Quadrats.
- 1 Diagonale teilt das Quadrat in zwei rechtwinklige gleichschenklige Dreiecke.
- Die Schnittpunkte der Winkelhalbierenden, Medianen und Mittelsenkrechten fallen alle in einem Punkt zusammen.
- Hat alle Eigenschaften eines Rechtecks, Parallelogramms und einer Raute.
Formel zur Berechnung der Diagonale eines Quadrats
Gemäß den Eigenschaften eines Quadrats sind zwei Diagonalen gleich groß, und eine Diagonale teilt das Quadrat in zwei gleich große Teile, die zwei gleichschenklige rechtwinklige Dreiecke bilden. Somit ist die Diagonale des Quadrats die Hypothenuse der beiden gleichschenkligen rechtwinkligen Dreiecke.
Um die Diagonale eines Quadrats zu berechnen, müssen Sie also nur den Satz des Pythagoras auf das rechtwinklige Dreieck anwenden.
Angenommen, Sie haben ein Quadrat ABCD mit der Seitenlänge a. Die Diagonale AC teilt das Quadrat in zwei rechtwinklige Dreiecke ABC und ACD.
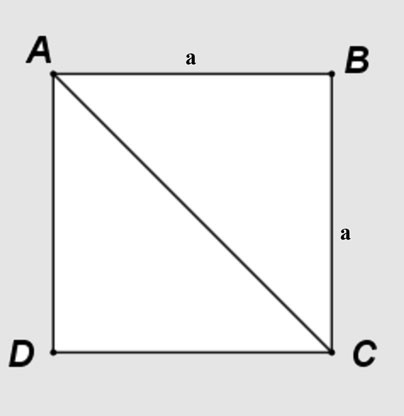
Anwendung des Satzes des Pythagoras auf das rechtwinklige gleichschenklige Dreieck ABC:
⇒ ⇒
Die Diagonale eines Quadrats hat also die Seitenlänge a:
Beispiel zur Berechnung der Diagonale eines Quadrats
Beispiel 1: Ein Quadrat hat eine Seitenlänge von 3 cm. Ist die Diagonale des Quadrats 6 cm, √18 cm, 5 cm oder 4 cm?
Lösung:
a) Wenn wir den Satz des Pythagoras im Quadrat ABC anwenden, erhalten wir:
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
Die Diagonale des Quadrats beträgt also √18 cm.
Beispiel 2:
Die Diagonale eines Quadrats beträgt 2dm. Die Seite des Quadrats ist: 1cm, 3/2cm, √2cm oder 4/3cm?
Preis:
Wenden Sie den Satz des Pythagoras auf das rechtwinklige Dreieck ABC an, aber diese Übung ergibt die Länge der Diagonale, d. h. AC = 2 cm, berechnen Sie die Seite AB.
Wir haben: AC² = AB² + BC² = 2AB (weil AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
So berechnen Sie die Diagonale eines Rechtecks
Ein Rechteck ist ein konvexes Viereck mit vier rechten Winkeln, es ist ein Parallelogramm mit zwei gleich langen Diagonalen.
Eigenschaften der Diagonalen eines Rechtecks
Die Diagonalen eines Rechtecks haben mehrere wichtige Eigenschaften, die beim Lösen von Problemen mit Rechtecken und ihren Diagonalen nützlich sind.
- Die Länge der Diagonale eines Rechtecks ist die Hypothenuse eines rechtwinkligen Dreiecks und entspricht daher der Quadratwurzel der Summe der Quadrate der beiden Seiten.
- Die Diagonale teilt das Rechteck in zwei rechtwinklige Dreiecke gleicher Fläche. Daher ist die Diagonale eines Rechtecks die Symmetrieachse des Rechtecks.
- Die beiden Diagonalen eines Rechtecks sind gleich groß und schneiden sich im Mittelpunkt jeder Linie und bilden 4 gleichschenklige Dreiecke.
Formel zur Berechnung der Diagonale eines Rechtecks
Aus den oben genannten Eigenschaften der Diagonale eines Rechtecks können wir den Satz des Pythagoras verwenden, um die Länge der Diagonale eines Rechtecks zu berechnen.
Angenommen, Sie haben ein Rechteck ABCD mit der Länge a und der Breite b und der Diagonale AC, wie unten gezeigt.
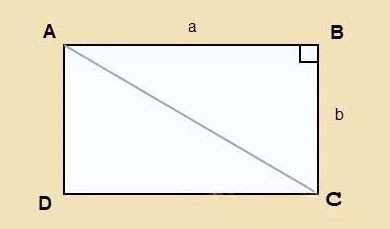
Wir wenden den Satz des Pythagoras auf das rechtwinklige Dreieck ABC an:
⇒ ⇒
Daher ist die Diagonale eines Rechtecks mit der Länge a und der Breite b:
Die Länge einer Diagonale eines Rechtecks ist also gleich der Quadratwurzel der Summe der Quadrate der beiden Seiten (Länge und Breite) des Rechtecks.
Daher können wir die Diagonale eines Quadrats oder Rechtecks berechnen, indem wir einfach den Satz des Pythagoras anwenden.
Beispiel zur Berechnung der Diagonale eines Rechtecks
Berechnen Sie die Länge der Diagonale eines Rechtecks mit einer Länge von 10 dm und einer Breite von 5 dm.
Lösung:
Die Länge der Diagonale des Rechtecks sei a (a > 0, dm)
Unter Anwendung des Satzes des Pythagoras beträgt die Länge der Diagonale des Rechtecks:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Beispiel zum Beweis, dass ein Viereck ein Rechteck ist.
Die Eigenschaften und Formel zur Berechnung der Diagonale eines Rechtecks können angewendet werden, um einige Probleme zu lösen, die beweisen, dass ein Viereck ein Rechteck ist.
Gegeben sei das Viereck ABCD mit zwei senkrecht zueinander stehenden Diagonalen. E, F, G und H seien jeweils die Mittelpunkte der Seiten AB, BC, CD und AD. Welche Form hat das Viereck EFGH? Warum?
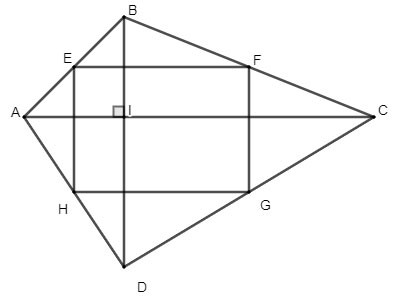
Lösung:
Da E der Mittelpunkt von AB ist, ist H der Mittelpunkt von AD
=> EH ist die Medianlinie des Dreiecks ABD.
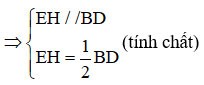 (1)
(1)
Da F der Mittelpunkt von BC ist, ist G der Mittelpunkt von CD
=> FG ist die Medianlinie des Dreiecks BCD
 (2)
(2)
Aus (1) und (2) =>
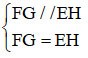
Betrachten Sie das Viereck EFGH.
FG // EH
FG = EH
=> EFGH ist ein Parallelogramm (Erkennungszeichen)
Auf der anderen Seite:
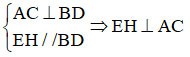
Außerdem hat:
E ist der Mittelpunkt von AB, F ist der Mittelpunkt von BC.
=> EF ist die Mediane des Dreiecks ABC
=> EF // AC
Aber EH ⊥ AC => EH ⊥ EF
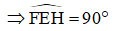
Parallelogramm EFGH hat einen rechten Winkel
=> EFGH ist ein Rechteck




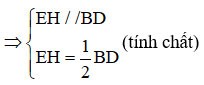 (1)
(1) (2)
(2)