Formel zur Berechnung der Diagonale einer Raute

Eine Raute ist ein Viereck mit vier gleich langen Seiten, ein Viereck mit zwei Diagonalen, die im Mittelpunkt jeder Linie senkrecht aufeinander stehen, ist eine Raute, ein Parallelogramm mit zwei gleich langen benachbarten Seiten ... Neben Quadraten, Rechtecken, Dreiecken ... ist die Raute eine der wichtigsten Formen in der Mathematik und im Leben.

Neben der Formel zur Berechnung des Umfangs und der Fläche einer Raute ist auch die Berechnung der Diagonale einer Raute – der Linie, die die gegenüberliegenden Eckpunkte der Raute miteinander verbindet – sehr wichtig.

Der folgende Artikel hilft Ihnen anhand konkreter Beispiele dabei, die Diagonale einer Raute zu berechnen. Bitte lesen Sie ihn.

Inhaltsverzeichnis

• Diagonale einer Raute
• Eigenschaften der Diagonalen einer Raute
• Formel zur Berechnung der Diagonale einer Raute
• Problem bei der Berechnung der Diagonale einer Raute

Diagonale einer Raute

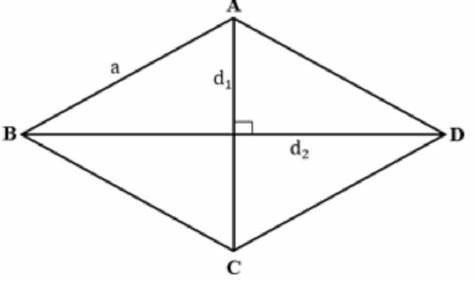
• Die Diagonale einer Raute ist die Linie, die zwei gegenüberliegende Eckpunkte der Raute verbindet.
• Eine Raute hat zwei Diagonalen, die sich im Mittelpunkt der Raute schneiden.
• Die Diagonale teilt die Raute in zwei gleichseitige Dreiecke mit gleicher Seitenlänge.

Eigenschaften der Diagonalen einer Raute

Die beiden Diagonalen einer Raute haben folgende Eigenschaften:

• Zwei gleich lange Diagonalen: Die beiden Diagonalen einer Raute sind gleich lang.
• Der Winkel zwischen zwei Diagonalen ist ein rechter Winkel: Die beiden Diagonalen einer Raute schneiden sich im Mittelpunkt der Raute und bilden einen rechten Winkel.
• Diagonalen sind die Symmetrieachsen einer Raute: Jede Diagonale einer Raute ist eine Symmetrieachse der Raute und teilt die Raute in zwei symmetrische Hälften.
• Diagonalen sind Diagonalen zweier gleichseitiger Dreiecke: Jede Diagonale einer Raute ist eine Diagonale zweier gleichseitiger Dreiecke, die aus gleich langen Seiten bestehen.
• Das Produkt der Längen der beiden Diagonalen ist gleich dem Produkt der Längen der beiden Seiten einer Raute: Das Produkt der Längen der beiden Diagonalen einer Raute ist gleich dem Produkt der Längen der beiden Seiten einer Raute. Das heißt, wenn wir die Diagonale mit d und die Seiten mit a und b bezeichnen, gilt d² = a² + b².

Diese Eigenschaften sind charakteristische Eigenschaften von Rauten und werden in vielen geometrischen Problemen mit Rauten verwendet.

Formel zur Berechnung der Diagonale einer Raute

Bitte betrachten Sie das folgende Beispiel, um die Formel zur Berechnung der Diagonale einer Raute abzuleiten.

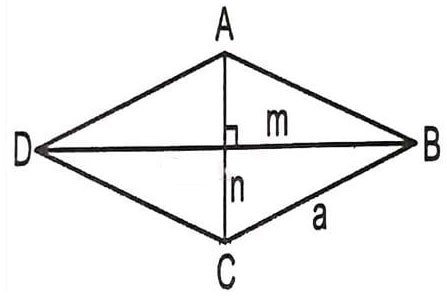
Angenommen, wir müssen die Länge der Diagonale einer Raute ABCD mit Seite a und einem Winkel ABC = 60 Grad berechnen -> wie lautet in diesem Fall die Formel zur Berechnung der Diagonale einer Raute?

Lösung:

Da ABCD eine Raute ist, sind alle Seiten gleich a.

Betrachten Sie das Dreieck ABC mit: AB = BC = a

Nochmals: ABC = 60 Grad => Dreieck ABC ist ein gleichseitiges Dreieck mit der Seite a.

=> AB = AC = BC = a

=> Die Länge der Diagonale der Raute beträgt AC = BD = a.

Die obige Lösung ist eine der einfachsten und am leichtesten verständlichen Formeln zur Berechnung der Diagonale einer Raute.

Formel zur Berechnung der Diagonale einer Raute bei Kenntnis der Fläche und der verbleibenden Diagonale

Aus der Formel zur Berechnung der Fläche einer Raute:

S = (axb) : 2

Die Formel für die Diagonallänge lautet:

a = S x 2 : b

oder

b = S x 2 : a

Darin:

• S ist die Fläche
• a und b sind die Längen der beiden Diagonalen

Nutze die geometrischen Eigenschaften einer Raute, um die Länge der Diagonale zu berechnen, ohne den Satz des Pythagoras zu verwenden. Genauer gesagt:

Die Diagonale einer Raute ist der Durchschnitt der beiden Höhen.

Diagonale = Quadratwurzel aus (lange Höhe + kurze Höhe)²

Die Diagonale einer Raute ist die Hälfte des Umfangs der Raute.

Diagonale = 1/2 x Umfang der Raute.

Problem bei der Berechnung der Diagonale einer Raute

Aufgabe 1: Bei einer Raute mit einer Fläche von 360 Quadratzentimetern beträgt die Länge einer Diagonale 24 Zentimeter. Berechnen Sie die Länge der zweiten Diagonale.

Lösung:

Nach der Formel für die Fläche einer Raute: axb : 2

Wir haben die zweite Diagonale: 360 x 2 : 24 = 30cm

Antwort: 30cm

Problem 2:

Eine Raute hat eine Fläche von 4 dm, die Länge einer Diagonale beträgt 3/5 dm. Berechne die Länge der zweiten Diagonale. Lösung:

Die Länge der zweiten Diagonale beträgt:

(4 x 2) : 3/5 =40/3 (dm)

Lektion 3: Die beiden Diagonalen einer Raute sind 160 cm und 120 cm lang. Berechne die Höhe der Raute. Das Verhältnis zwischen Höhe und Länge der Seiten beträgt 24:25.

Lösung:

Die Fläche der Raute beträgt: 160,120:2 = 9 600 (cm²).

Da das Verhältnis zwischen Höhe und Seitenlänge einer Raute 24:25 beträgt, können wir davon ausgehen, dass die Höhe der Raute 24a und die Seitenlänge der Raute 25a beträgt.

Dann haben wir die Fläche der Raute: 25a.24a = 9 600 a2 = 16 a = 4 cm.

Die Höhe der Raute beträgt: 24,4 = 96 (cm).

Die Höhe der Raute beträgt also 96 cm.

Lektion 4: 

Gegeben sei die Raute ABCD mit einer Seitenlänge von 12,5 cm und einer Höhe von 6,72 cm. AC ist kleiner als BD. Wie lang sind die Diagonalen AC und BD?

Preis:

Wenden Sie die Formel an, um die Fläche einer Raute zu berechnen: S = ha = 6,72 x 12,5 = 84 cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Sei O der Schnittpunkt der beiden Diagonalen einer Raute.

Wir haben AOB ist ein rechtwinkliges Dreieck bei O, also AB2 = OA2 + OB2

Dabei gilt: OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Laut Problemstellung BD > AC) (2)

Aus (1) und (2) folgt:

BD = 24, AC = 7 cm.

Lektion 5: 

Die Raute ABCD hat eine Seitenlänge von 10 Einheiten. Berechnen Sie die Länge der Diagonale der Raute.

Lösung: Die Länge der Diagonale der Raute ABCD beträgt:

Diagonale = Quadratwurzel aus 2(10²) = Quadratwurzel aus 200 = 14,14 Längeneinheiten.

Die Länge der Diagonale der Raute ABCD beträgt also 14,14 Längeneinheiten.

Lektion 6:

Die Raute ABCD hat eine Diagonale von 12 Einheiten. Berechnen Sie den Umfang der Raute.

Lösung: Da eine Raute vier gleich lange Seiten hat, ist ihr Umfang die Summe der Längen der vier Seiten, d. h.:

Umfang = 4 x Seitenlänge = 4 x 6 = 24 Längeneinheiten.

Der Umfang der Raute ABCD beträgt also 24 Längeneinheiten.