Was ist eine rationale Zahl? Was ist eine irrationale Zahl?

Definitionen und Formeln rationaler und irrationaler Zahlen sind wichtige Kenntnisse in der Mathematik, die Schüler verstehen müssen, um eine solide mathematische Grundlage zu haben. Der folgende Artikel stellt Ihnen die Definitionen, Eigenschaften und mathematischen Formen rationaler und irrationaler Zahlen vor. Bitte lesen Sie ihn.

Rationale Zahlen, irrationale Zahlen

• Was ist eine rationale Zahl?
  • Klassifizierung rationaler Zahlen
  • Darstellung rationaler Zahlen auf einer Zahlengeraden
  • Addieren und Subtrahieren rationaler Zahlen
  • Multiplizieren und dividieren Sie rationale Zahlen
  • Absolutwert einer rationalen Zahl
  • Vergleichen Sie zwei rationale Zahlen
  • Formel zur Berechnung der Potenz einer rationalen Zahl
• Was ist eine irrationale Zahl?
  • Konzept der irrationalen Zahlen
  • Eigenschaften irrationaler Zahlen
• Was ist der Unterschied zwischen rationalen und irrationalen Zahlen?
• Beziehung von Zahlenmengen
• Übungen zu rationalen Zahlen

Was ist eine rationale Zahl?

- Rationale Zahlen sind die Menge der Zahlen, die als Brüche (Quotienten) geschrieben werden können. Das heißt, eine rationale Zahl kann durch eine unendliche periodische Dezimalzahl dargestellt werden.

- Rationale Zahlen werden als geschrieben, wobei a und b ganze Zahlen sind, aber b ungleich 0 sein muss.

- ist die Menge der rationalen Zahlen.

=> Menge der rationalen Zahlen: .

Zum Beispiel: , , … sind rationale Zahlen.

• Jede ganze Zahl a ist eine rationale Zahl, da die ganze Zahl a in der Form geschrieben werden kann.

Beispiel: Wir haben rationale Zahlen.

Wir haben:

Kommentar: sind alles rationale Zahlen.

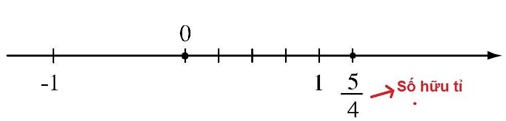
Klassifizierung rationaler Zahlen

Rationale Zahlen werden in zwei Typen unterteilt: negative rationale Zahlen und positive rationale Zahlen. Im Einzelnen:

• Negative rationale Zahlen: Schließen rationale Zahlen kleiner als 0 ein.
• Positive rationale Zahlen: Schließen rationale Zahlen größer als 0 ein.

Hinweis: Die Zahl 0 ist weder eine negative noch eine positive rationale Zahl.

Natur

• Die Menge der rationalen Zahlen ist eine abzählbare Menge.
• Kommutativgesetz:
• Additionseigenschaft mit 0:
• Kombinierte Eigenschaften:

Darstellung rationaler Zahlen auf einer Zahlengeraden

- Um rationale Zahlen auf der Zahlengeraden darzustellen, berücksichtigen wir diese Faktoren:

Schritt 1: Schreiben Sie die rationale Zahl als Bruch

Schritt 2: Teilen Sie das Einheitsliniensegment in b gleiche Teile, um ein neues Einheitssegment zu erhalten, das die alte Einheit darstellt.

Schritt 3: Die rationale Zahl wird durch Punkt A dargestellt, der eine Entfernung von einer neuen Einheit vom Punkt 0 hat.

• A steht links von 0, wenn es eine negative Zahl ist.
• A steht rechts von 0, wenn es eine positive Zahl ist.

Beispiel: In der Abbildung stellt der Punkt P die rationale Zahl dar:

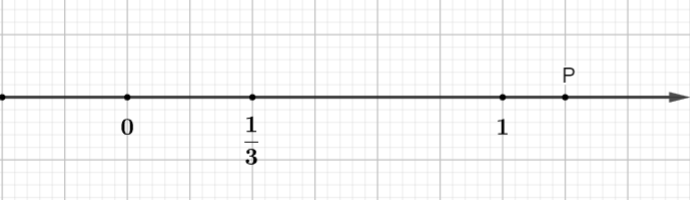
Anweisen

Das Einheitsliniensegment ist in 6 gleiche Teile unterteilt (die neue Einheit ist 1/6 der alten Einheit).

Punkt P liegt in einer Entfernung von 7 neuen Einheiten von Punkt O.

Und Punkt P liegt rechts von Punkt O, also ist P eine positive rationale Zahl.

P stellt also eine rationale Zahl dar.

Addieren und Subtrahieren rationaler Zahlen

i) Regeln zum Addieren und Subtrahieren zweier rationaler Zahlen

Wir können zwei rationale Zahlen x und y addieren und subtrahieren, indem wir sie als zwei Brüche schreiben und dann die Regeln zum Addieren und Subtrahieren von Brüchen anwenden.

Bei uns haben wir:

ii) Eigenschaften

- Die Addition rationaler Zahlen hat die Eigenschaften der Addition von Brüchen: kommutativ, assoziativ, Addition mit 0, Addition mit Gegensätzen.

- Wir haben:

a) Kommutativgesetz:

b) Assoziative Eigenschaften:

c) Addiere 0:

d) Addieren Sie die Gegenzahl:

iii, Übergangsregeln

Wenn wir einen Term von einer Seite einer Gleichung auf die andere verschieben, müssen wir das Vorzeichen dieses Terms ändern.

In Q haben wir eine algebraische Summe, in der wir Terme vertauschen und Klammern setzen können, um Terme beliebig zu gruppieren, wie algebraische Summen in der Menge der ganzen Zahlen.

• Mit wenn dann
• Bei uns haben wir:

Multiplizieren und dividieren Sie rationale Zahlen

i) Regeln zum Multiplizieren und Dividieren zweier rationaler Zahlen

- Wir können zwei rationale Zahlen multiplizieren und dividieren, indem wir sie als Brüche schreiben und dann die Regeln zum Multiplizieren und Dividieren von Brüchen anwenden.

• Bei uns haben wir:
• Bei uns haben wir:

Zum Beispiel:

Multiplizieren Sie rationale Zahlen: 

Dividieren Sie rationale Zahlen: 

ii) Eigenschaften

- Die Multiplikation rationaler Zahlen hat auch die gleichen Eigenschaften wie die Multiplikation von Brüchen: Kommutativ, Assoziativ, Multiplikation mit 1 und Distributivgesetz der Multiplikation über die Addition.

- Jede von Null verschiedene rationale Zahl hat eine Inverse.

- Wir haben:

• Kommutativgesetz: .
• Assoziative Eigenschaften: .
• Eigenschaft der Multiplikation mit 1: .
• Distributive Eigenschaften: .
• Mit . Die Umkehrung von a ist .

Absolutwert einer rationalen Zahl

- Der Absolutwert einer rationalen Zahl a, bezeichnet mit , ist der Abstand vom Punkt a zum Punkt 0 auf der Zahlengeraden.

Zum Beispiel:

(Weil )

(Weil )

Vergleichen Sie zwei rationale Zahlen

- Bei zwei beliebigen rationalen Zahlen gilt immer entweder oder oder .

- Um zwei rationale Zahlen zu vergleichen, gehen wir wie folgt vor:

• Schreiben Sie es als 2 Brüche mit demselben positiven Nenner:
• Vergleichen Sie die Zähler als ganze Zahlen a, b:

Beispiel: Vergleichen Sie zwei rationale Zahlen: und

Wir haben:

Weil es gut ist.

Formel zur Berechnung der Potenz einer rationalen Zahl

Formeln zur Berechnung von Potenzen rationaler Zahlen, die Sie sich merken müssen

• Produkt zweier Potenzen mit gleicher Basis:
• Macht der Macht
• Leistung eines Produkts
• Potenz eines Quotienten

Was ist eine irrationale Zahl?

Konzept der irrationalen Zahlen

• Wenn man von rationalen Zahlen spricht, muss man zwangsläufig auch von irrationalen Zahlen sprechen. Dabei handelt es sich um Zahlen, die als unendliche, sich nicht wiederholende Dezimalzahlen geschrieben und mit gekennzeichnet sind.
• Reelle Zahlen, die keine rationalen Zahlen sind, können nicht als Verhältnisse dargestellt werden.

Beispiel: 3,145248… ist eine irrationale Zahl.

Eigenschaften irrationaler Zahlen

Die Menge der irrationalen Zahlen ist eine überabzählbare Menge.

Zum Beispiel:

Irrationale Zahlen: 0,1010010001000010000010000001… (das ist eine unendliche, sich nicht wiederholende Dezimalzahl)

Anzahl der Quadratwurzeln: √2 (Quadratwurzel)

Pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Was ist der Unterschied zwischen rationalen und irrationalen Zahlen?

• Rationale Zahlen umfassen nicht endende, sich wiederholende Dezimalzahlen, während irrationale Zahlen nicht endende, sich nicht wiederholende Dezimalzahlen sind.
• Rationale Zahlen sind einfach nur Brüche, während irrationale Zahlen viele verschiedene Zahlenarten haben.
• Rationale Zahlen sind zählbare Zahlen, während irrationale Zahlen überzählige Zahlen sind.

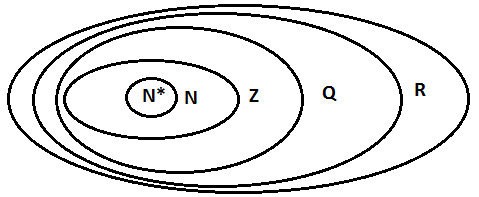
Beziehung von Zahlenmengen

Symbole von Zahlenmengen:

• N: Menge der natürlichen Zahlen
• N*: Menge der natürlichen Zahlen ungleich 0
• Z: Menge von Ganzzahlen
• F: Die Menge der rationalen Zahlen
• I: Menge der irrationalen Zahlen

Wir haben: R = Q ∪ I.

Menge N; Z; Q; R.

Dann lautet die Inklusionsbeziehung zwischen den Zahlenmengen: N ⊂ Z ⊂ Q ⊂ R

Übungen zu rationalen Zahlen

Form 1: Berechnungen mit rationalen Zahlen durchführen

Lösungsweg: Um Rechenaufgaben mit rationalen Zahlen zu lösen, wandeln Sie die rationalen Zahlen zunächst in Brüche um und wenden Sie anschließend die Rechenregeln bei der Addition, Subtraktion, Multiplikation und Division rationaler Zahlen an.

Beispiel: Berechnen  

Antwort:

Form 2: Darstellung rationaler Zahlen auf der Zahlengeraden

Lösung: Sie müssen feststellen, ob die rationale Zahl eine positive oder eine negative rationale Zahl ist, und dann mit den nächsten Schritten fortfahren:

• Wenn die rationale Zahl a/b eine positive rationale Zahl ist: Teilen Sie auf der Zahlengeraden in positiver Achsenrichtung die Länge von 1 Einheit in b gleiche Teile. Wählen Sie dann einen Punkt in positiver Achsenrichtung, zeigen Sie auf einen Teil und bestimmen Sie die Position der rationalen Zahl a/b.
• Wenn die rationale Zahl a/b eine negative rationale Zahl ist: Teilen Sie auf der Zahlengeraden in negativer Richtung der x-Achse die Länge einer Einheit in b gleiche Teile. Wählen Sie dann einen Punkt in negativer Richtung der ox-Achse, zeigen Sie auf einen Teil und bestimmen Sie die Position der rationalen Zahl a/b.

Form 3: Vergleichen rationaler Zahlen

Lösung: Wandeln Sie die gegebenen rationalen Zahlen in Brüche mit gleichem positiven Nenner um und vergleichen Sie anschließend die Zähler. Auf einer fortgeschritteneren Ebene können wir die Antwort durch Vergleichen mit Zwischenbrüchen finden.

Form 4: Bestimmen Sie, ob eine rationale Zahl negativ, positiv oder 0 ist

Lösungsmethode: Um Übungen vom Typ 4 zu lösen, müssen die Schüler anhand der Eigenschaften rationaler Zahlen feststellen, ob die rationale Zahl negativ, positiv oder 0 ist.

Beispiel: Gegeben sei die rationale Zahl x = (a – 25)/29. Bestimmen Sie den Wert von a so, dass:

• x ist negativ
• x ist positiv
• x = 0

Antwort:

x ist eine negative Zahl => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x ist eine positive Zahl => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Form 5: Finden Sie rationale Zahlen im Intervall gemäß den gegebenen Bedingungen

Lösung: Wenn die Frage das Finden rationaler Zahlen innerhalb eines Intervalls gemäß gegebener Bedingungen erfordert, müssen wir die rationalen Zahlen in denselben Zähler oder Nenner einsetzen, um die Antwort zu finden.

Beispiel: Ermitteln Sie den Wert von m für größer als und kleiner als

Antwortleitfaden

Wandeln Sie Brüche wie folgt in gemeinsame Nenner um:

Gemeinsamer Nenner: 18

Gemäß der Frage haben wir:

Form 6: Finden Sie x mit rationalen Zahlen

Methode zum Lösen mathematischer Probleme: Um x in mathematischen Problemen mit rationalen Zahlen zu finden, muss man den gemeinsamen Nenner reduzieren und x auf eine Seite und die verbleibenden Terme auf 1 umwandeln. Berechnen Sie von dort aus den Wert von x.

Beispiel: Finden Sie x, wenn Sie x kennen. (2/ 3) + 5/ 6 = 1/ 8

Antwort:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 , 3 / 24 , 2

=> 23/16

Form 7: Finden Sie a, sodass der Ausdruck eine Ganzzahl ist

Methode zur Lösung mathematischer Probleme: Um a zu finden, müssen wir das Teilbarkeitszeichen verwenden, wenn der Zähler kein a enthält. Enthält der Zähler a, müssen wir das Teilbarkeitszeichen verwenden oder den Zähler entsprechend dem Nenner trennen. Wenn sowohl a als auch b gefunden werden müssen, müssen wir a oder b gruppieren und für die Berechnung in eine Bruchform umwandeln.

Beispiel: Finden Sie die Ganzzahl a unter der Bedingung, dass 8/(a – 1) eine Ganzzahl ist

Antwort:

Bedingung: a – 1 ≠ 0 => a ≠ 1

Sei a eine ganze Zahl => 8 ist durch (a – 1) teilbar

=> (a – 1) ist ein Faktor von 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Hoffentlich hat Ihnen der obige Artikel geholfen zu verstehen, was rationale Zahlen sind, was irrationale Zahlen sind, welche Arten rationaler Zahlen es gibt, was rationale Zahlensymbole sind und wie Sie rationale Zahlen erkennen, um Probleme einfach zu lösen.

Zusätzlich zu den oben genannten Kenntnissen über irrationale Zahlen und rationale Zahlen können Sie auf einige andere mathematische Kenntnisse zurückgreifen, wie etwa Brüche , gemischte Zahlen , Dezimalzahlen …