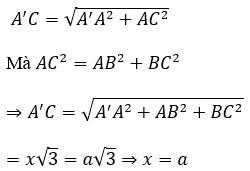Ein Prisma ist ein Polygon mit zwei parallelen und gleich großen Grundflächen und parallelogrammförmigen Seitenflächen.
Kommentar:
- Die Seitenflächen eines Prismas sind gleich und parallel zueinander.
- Die Seitenflächen sind Parallelogramme.
- Die beiden Grundflächen eines Prismas sind zwei gleich große Polygone.
Wie lautet die Formel zur Berechnung des Volumens eines Prismas (V-Prisma) bzw. die Formel zur Berechnung des Volumens eines vertikalen Prismas? Bitte lesen Sie den folgenden Artikel.
Inhaltsverzeichnis
1. Volumen eines vertikalen Prismas
Formel zur Berechnung des Volumens eines vertikalen Prismas:
Das Volumen eines geraden Prismas ist gleich dem Produkt aus der Grundfläche multipliziert mit der Höhe.
Dort drin
Vist das Volumen des Prismas (Einheit m3)Bist die Grundfläche (Einheit m2)hist die Höhe des Prismas (Einheit m)
3. Klassifizierung von Prismen
Normales Prisma
Es handelt sich um ein vertikales Prisma mit einer regelmäßigen polygonalen Grundfläche. Die Seitenflächen des Prismas sind alle gleich große Rechtecke. Beispielsweise: ein regelmäßiges dreieckiges Prisma, ein regelmäßiges Viereck... dann verstehen wir es als regelmäßiges Prisma.
Eine regelmäßige vierseitige Basis wird als regelmäßiges vierseitiges Prisma bezeichnet.
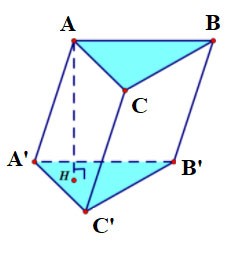
Dreieckiges Prisma
- Ein dreieckiges Prisma hat 5 Flächen, 9 Kanten und 6 Eckpunkte.
- Die beiden Grundflächen sind dreieckig und parallel zueinander; jede Seitenfläche ist ein Rechteck;
- Die Seiten sind gleich;
- Die Höhe eines dreieckigen Prismas entspricht der Länge einer Seite.
Zum Beispiel:
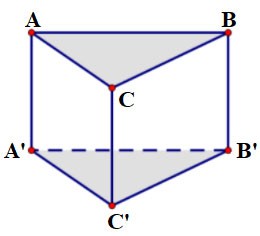
Das dreieckige Prisma ABC.A'B'C' hat:
- Die untere Basis ist das Dreieck ABC, die obere Basis ist das Dreieck A'B'C';
Die Seitenflächen sind Rechtecke: AA'B'B, BB'C'C, CC'A'A;
- Kanten:
- Basiskanten: AB, BC, CA, A'B', B'C', C'A'
- Seiten: AA', BB', CC';
- Eckpunkte: A, B, C, A', B', C'.
- Die Höhe ist die Länge einer Seite: AA‘ oder BB‘ oder CC‘.
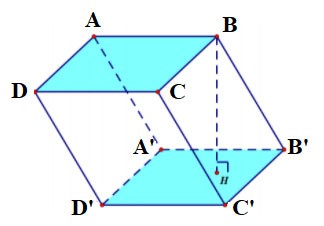
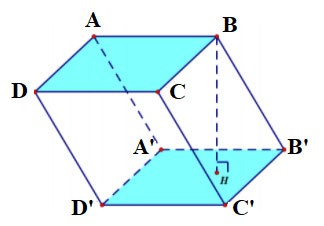
Vierseitiges Prisma
- Ein vierseitiges Prisma hat 6 Flächen, 12 Kanten und 8 Eckpunkte.
- Die beiden Grundflächen sind jeweils Vierecke und parallel zueinander. Jede Seitenfläche ist ein Rechteck.
- Die Seiten sind gleich.
- Die Höhe eines vierseitigen Prismas entspricht der Länge einer Seite.
Zum Beispiel:
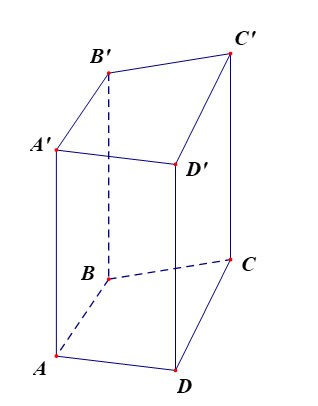
Das vierseitige Prisma ABCD.A'B'C'D' hat:
- Die untere Basis ist das Viereck ABCD, die obere Basis ist das Viereck A'B'C'D';
Die Seitenflächen sind Rechtecke: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Kanten:
+ Basiskanten: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Seitenkanten: AA', BB', CC', DD' sind gleich.
- Eckpunkte: A, B, C, D, A', B', C', D'.
- Die Höhe ist die Länge einer Seite: AA‘ oder BB‘ oder CC‘ oder DD‘.
Hinweis: Auch rechteckige Prismen und Würfel sind vierseitige Prismen.
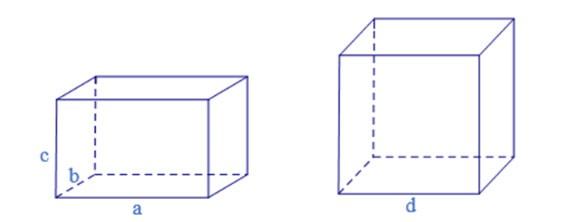
Rechtes Prisma
Wenn die Seitenkanten eines Prismas senkrecht zur Grundfläche stehen, spricht man von einem geraden Prisma.
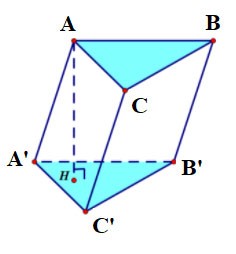
Notiz:
Wenn die Basis ein Rechteck ist, wird der vertikale Zylinder des Vierecks als rechteckiger Kasten bezeichnet.
Wenn ein viereckiger Zylinder 12 Seiten der Länge a hat, dann nennt man ihn Würfel.
Vergleichen Sie das rechte Prisma und das normale Prisma:
| DEFINIEREN: |
NATUR |
| + Ein vertikales Prisma ist ein Prisma, dessen Seite senkrecht zur Basis steht. |
+ Die Seitenflächen eines vertikalen Prismas sind rechteckig.
+ Die Seitenflächen des Prismas stehen senkrecht auf der Grundfläche.
+ Höhe ist die Seite
|
| + Ein reguläres Prisma ist ein vertikales Prisma, dessen Basis ein reguläres Polygon ist. |
+ Die Seitenflächen eines Prismas sind alle gleich große Rechtecke.
+ Höhe ist die Seite
|
4. Beispiel zur Berechnung des Volumens eines vertikalen Prismas
Beispiel 1:
Gegeben ist das Prisma ABC.A'B'C', dessen Basis ABC ein gleichseitiges Dreieck mit der Seitenlänge a = 2 cm und der Höhe h = 3 cm ist. Berechnen Sie das Volumen dieses Prismas.
Preis:
Da die Basis ein gleichseitiges Dreieck mit der Seite a ist, beträgt die Fläche:
Zu diesem Zeitpunkt beträgt das Volumen des Prismas:
Beispiel 2:
Aufgabe 1: Gegeben sei ein vertikaler Kasten mit den Kanten AB = 3a, AD = 2a, AA'= 2a. Berechnen Sie das Volumen des Blocks A'.ACD'
Anweisen:
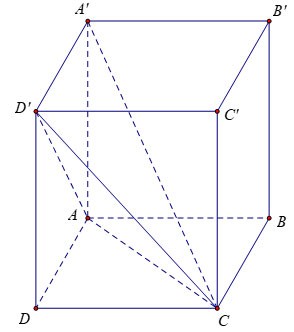
Da die Seitenfläche ADD'A' ein Rechteck ist, gilt:
Beispiel 3 : Gegeben sei ein vertikales Prisma ABC.A'B'C', dessen Grundfläche ein gleichseitiges Dreieck mit der Seitenlänge a√3 ist. Der Winkel zwischen Prisma und Grundfläche beträgt 60º. M sei der Mittelpunkt von BB'. Berechnen Sie das Volumen der Pyramide MA'B'C'.
Preis:
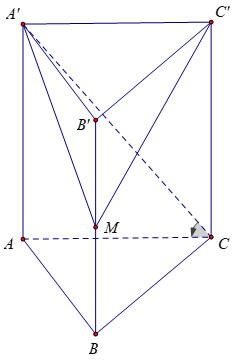
Daher können wir schlussfolgern, dass
Wir haben:
Beispiel 4:
Gegeben sei ein regelmäßiges vierseitiges Prisma ABCD.A'B'C'D' mit einer Basiskante von a und einer Fläche (DBC') mit der Basis ABCD in einem Winkel von 60º. Berechnen Sie das Volumen des Prismas ABCD.A'B'C'D.
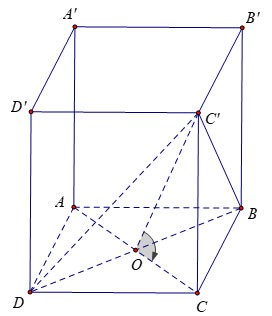
Wir haben: im Mittelpunkt O des Quadrats ABCD.
Auf der anderen Seite deshalb
Schließen
Auch:
Beispiel 5:
Berechnen Sie das Volumen V des Würfels ABCD.A'B'C'D', wobei AC'=a√3 gilt
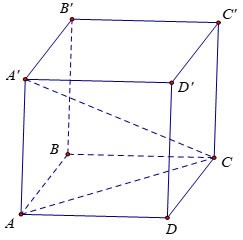
Preis:
Sei x die Länge der Seite des Würfels.
Betrachten Sie das Dreieck AA'C, das im rechten Winkel zu A liegt, mit:
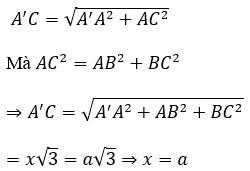
Daher beträgt das Volumen des Würfels V=a^3.
Zusätzlich zu der Formel zur Berechnung des Volumens eines Prismas weiter oben können Sie weitere Artikel zur Formel zur Berechnung des Volumens eines Rotationskörpers und zur Formel zur Berechnung der Fläche und des Umfangs eines Kreises lesen …