Der Höhenschnittpunkt eines Dreiecks ist der Schnittpunkt der drei Höhenlinien , d. h. der Schnittpunkt der Linien, die von jedem Scheitelpunkt des Dreiecks zur gegenüberliegenden Seite einen rechten Winkel bilden. Die Länge der Höhenlinie ist der Abstand zwischen Scheitelpunkt und Basis.
Orthozentrum eines Dreiecks
Was ist das Orthozentrum?
Die drei Höhen eines Dreiecks treffen sich in einem Punkt. Dieser Punkt wird als Höhenschnittpunkt des Dreiecks bezeichnet .
Konkret: In der Zeichnung sind die Höhen, also die Höhenschnittpunkte des Dreiecks, eingezeichnet.
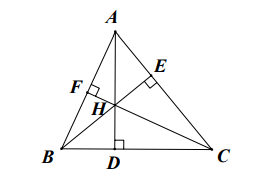
So bestimmen Sie den Orthozentrum eines Dreiecks
Um den Höhenschnittpunkt eines Dreiecks zu bestimmen, suchen wir den Schnittpunkt der beiden Höhen in diesem Dreieck.
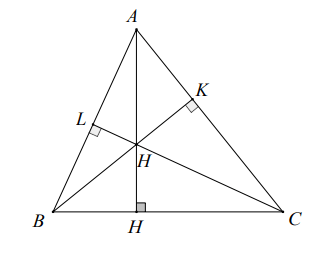
Hinweis: a) Handelt es sich bei dem Dreieck um ein spitzwinkliges Dreieck, liegt der Höhenschnittpunkt innerhalb des Dreiecks.
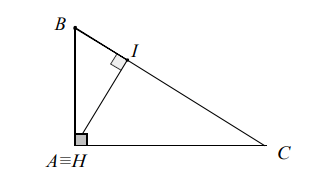
b) Wenn das Dreieck ein rechtwinkliges Dreieck bei ist, dann fällt der Höhenschnittpunkt mit dem Punkt zusammen.
c) Wenn ein Dreieck ein stumpfwinkliges Dreieck ist, dann liegt der Höhenschnittpunkt außerhalb des Dreiecks.
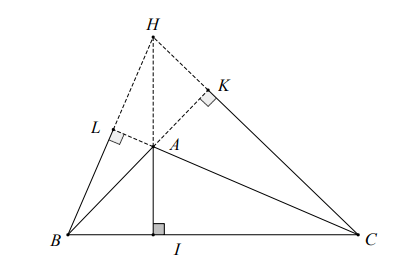
Eigenschaften des Orthozentrums eines Dreiecks
Eigenschaft 1: In einem gleichseitigen Dreieck sind der Schwerpunkt, der Höhenschnittpunkt, ein Punkt im gleichen Abstand von den drei Eckpunkten des Dreiecks, ein Punkt innerhalb des Dreiecks und im gleichen Abstand von den drei Seiten des Dreiecks vier zusammenfallende Punkte.
Eigenschaft 2: Der Höhenschnittpunkt schneidet die Mittelsenkrechte zweier Seiten in zwei gleich lange Abschnitte. Das bedeutet, dass der Höhenschnittpunkt von den Eckpunkten des Dreiecks gleich weit entfernt ist.
Eigenschaft 3: Der Höhenschnittpunkt ist der Mittelpunkt des Umkreises eines Dreiecks. Das bedeutet, wenn wir einen Kreis zeichnen, der durch die drei Eckpunkte eines Dreiecks verläuft, ist der Höhenschnittpunkt der Mittelpunkt dieses Kreises.
Eigenschaft 4: Der Höhenschnittpunkt eines spitzen Dreiecks liegt innerhalb des Dreiecks, während der Höhenschnittpunkt eines stumpfen Dreiecks außerhalb des Dreiecks liegt.
Eigenschaft 5: Der Höhenschnittpunkt eines rechtwinkligen Dreiecks fällt mit dem Scheitelpunkt des rechten Winkels dieses rechtwinkligen Dreiecks zusammen.
Eigenschaft 6: Der Höhenschnittpunkt ist der einzige Punkt in einem Dreieck, bei dem die Summe der Längen der Linien, die vom Höhenschnittpunkt zu den Eckpunkten des Dreiecks gezogen werden, am kleinsten ist. Das bedeutet, dass der Höhenschnittpunkt den Eckpunkten des Dreiecks am nächsten liegt.
Eigenschaft 7: Der Höhenschnittpunkt ist gleichzeitig der Mittelpunkt des Umkreises des Dreiecks, also des größten Kreises, der durch die drei Eckpunkte des Dreiecks gezogen werden kann.
Übungen zur Bestimmung und zum Beweis des Höhenschnittpunkts eines Dreiecks
Beispiel: Gegeben sei ein nicht rechtwinkliges Dreieck. Nennen Sie dessen Höhenschnittpunkt. Bestimmen Sie die Höhen des Dreiecks. Bestimmen Sie von dort aus den Höhenschnittpunkt des Dreiecks.
Lösungsleitfaden
Illustration

Lassen Sie die Füße der Senkrechten sein, die von ΔABC gezogen werden.
Berücksichtigen Sie ΔHBC mit:
also ist AD die Höhe von H bis BC.
bei F ist BA also die Höhe von B bis HC
bei E ist CA also die Höhe von C bis HB.
schneiden sich bei A, also ist A der Orthomittelpunkt von ΔHCB.
Beispiel: Gegeben ist ein rechtwinkliges Dreieck mit der Höhe . Der Mittelpunkt von sei , der Mittelpunkt von ist . Bestimmen Sie den Höhenschnittpunkt des Dreiecks .
Lösungsleitfaden
Betrachten Sie das Unterproblem: Wenn das Dreieck und AC als Mittelpunkte hat, dann und .
Tatsächlich nehmen wir auf dem gegenüberliegenden Strahl des Strahls einen Punkt, so dass
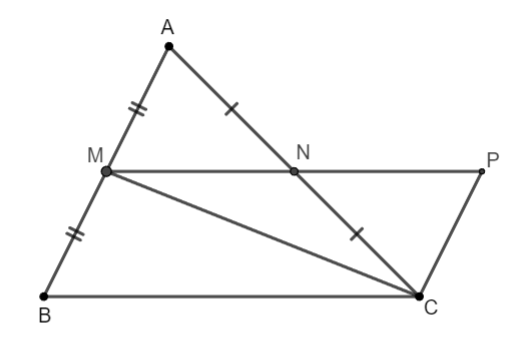
Betrachten Sie das Dreieck AMN und das Dreieck CPN.
(Gegenteil)
, (zwei Seiten und zwei entsprechende Winkel)
Zwei Winkel befinden sich in abwechselnden Positionen, so
=> (zwei abwechselnde Innenwinkel)
Betrachten Sie das Dreieck BMC und das Dreieck PCM.
(cmt)
MC ist eine gemeinsame Kante
, (entsprechende Seiten und Winkel)
Zwei Winkel befinden sich in abwechselnden Positionen, so
Wir haben wieder
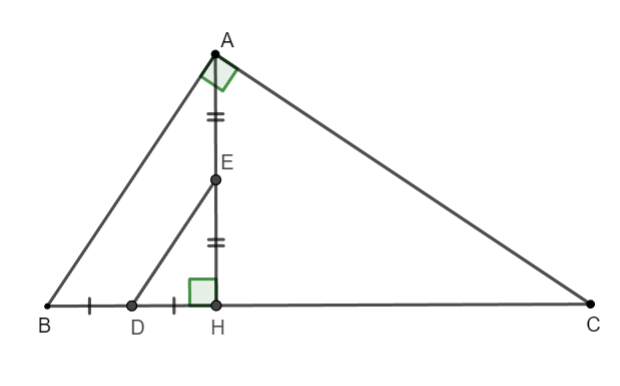
Betrachten Sie das Dreieck HAB mit:
(wie oben bewiesen)
Betrachten Sie das Dreieck ADE.
auf der anderen Seite und
ist die Höhe des Dreiecks ADE
C ist der Schnittpunkt von AC und DC
=> C ist der Höhenschnittpunkt des Dreiecks ADE
Beispiel: Bei einem Dreieck bei A schneidet die Höhe die Mediane bei . Beweisen und berechnen?
Anweisen
Illustration
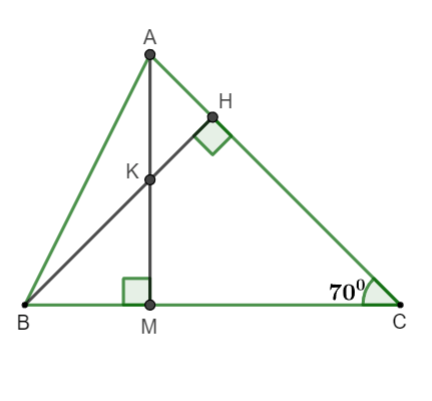
Da der Saldo bei A liegt und AM der Medianwert ist
⇒ AM ist auch die Höhe, die BC entspricht
bei M.
Andererseits ist K also der Höhenschnittpunkt.
Daher gehört K zur Höhe von C von ∆ABC.
Wir haben: