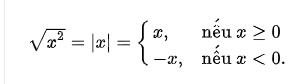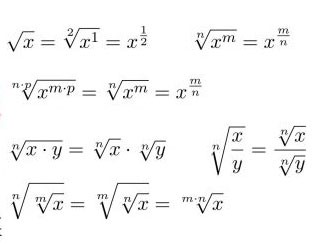Quadratwurzel, wie man die Quadratwurzel berechnet

Die Quadratwurzel ist eine wichtige mathematische Erkenntnis, die Schüler im Lernprozess nutzen. Der folgende Artikel erklärt Ihnen die Definition der Quadratwurzel. Wie berechnet man die Quadratwurzel einer Zahl? Bitte lesen Sie weiter.

Inhaltsverzeichnis

• Was ist die Quadratwurzel?
• Die grundlegendsten Quadratwurzelberechnungen
  • Quadratwurzeltabelle
• So berechnen Sie die Quadratwurzel ohne Taschenrechner
  • Finden Sie die Quadratwurzel einer Ganzzahl
  • Finden Sie die Quadratwurzel anderer Zahlen
• So vergleichen Sie Quadratwurzeln 

Was ist die Quadratwurzel?

Die Quadratwurzel einer Zahl a ist eine Zahl x, bei der x2 = a, oder anders ausgedrückt, die Zahl x, deren Quadratwert = a.

Beispielsweise sind 2 und −2 Quadratwurzeln von 2, da 2² = (−2)² = 4.

Das Wurzelzeichen wird mit √ gekennzeichnet.

• Jede nicht-negative reelle Zahl a hat eine eindeutige nicht-negative Quadratwurzel, die als arithmetische quadratische Wurzel bezeichnet wird.

Beispielsweise ist die arithmetische Quadratwurzel von 16 4, dargestellt durch √16 = 4, da 4² = 4 × 4 = 16 und 4 eine nicht-negative Zahl ist.

Jede positive Zahl a hat zwei Quadratwurzeln: √a ist die positive Quadratwurzel und −√a ist die negative Quadratwurzel. Beide werden mit ± √a bezeichnet.

Die grundlegendsten Quadratwurzelberechnungen

Merken Sie sich einige grundlegende und häufigste Quadratzahlen, damit Sie beim Ziehen der Quadratwurzel schneller im Kopf rechnen können:

0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289

Zu den grundlegenden Formeln für Quadratwurzeln, die sich jeder merken sollte, gehören:

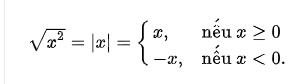
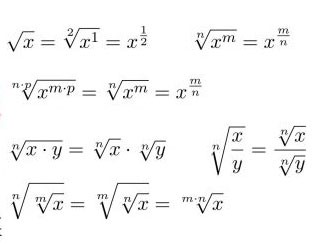
Quadratwurzeltabelle

Die Quadratwurzeltabelle ist in Zeilen und Spalten unterteilt, sodass die Quadratwurzel von Zahlen größer als 1 und kleiner als 100 direkt ermittelt werden kann.

In der Tabelle sind in den Spalten 0 bis 9 die Quadratwurzeln von maximal dreistelligen Zahlen im Bereich von 1,00 bis 99,9 angegeben. Anschließend folgen neun Korrekturspalten, mit denen die letzte Ziffer der Quadratwurzeln von vierstelligen Zahlen im Bereich von 1,000 bis 99,99 korrigiert werden kann.

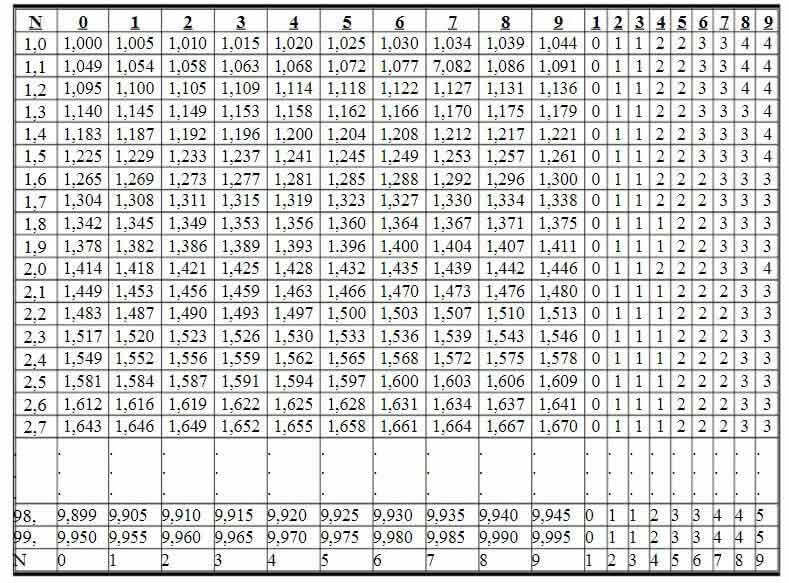
Beispiel 1: Suchen

→ Lösung:

Am Schnittpunkt der Zeilen 1,4 und Spalte 1 sehen wir die Zahl 1,187

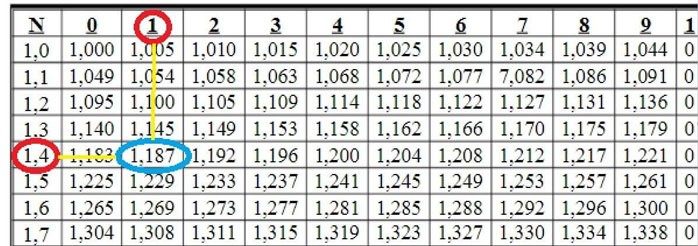
Also

Beispiel 2: 

Finden

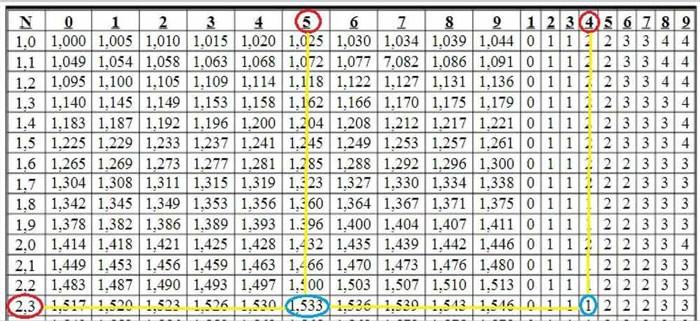
Am Schnittpunkt der Zeilen 2, 3 und Spalte 5 sehen wir die Zahl 1,533. Wir haben

Als nächstes sehen wir am Schnittpunkt der Zeilen 2, 3 und Spalte 4 die Zahl 1. Diese Zahl 1 wird verwendet, um die letzte Ziffer der Zahl zu korrigieren. Das heißt: 1,533 + 0,001 = 1,534

Also

So berechnen Sie die Quadratwurzel ohne Taschenrechner

Finden Sie die Quadratwurzel einer Ganzzahl

Finden Sie die Quadratwurzel durch Multiplikation.

Die Quadratwurzel einer Zahl ist die Zahl, die, wenn Sie die Zahl mit sich selbst multiplizieren, die ursprüngliche Zahl ergibt.

Das bedeutet also: „Welche Zahl können Sie mit sich selbst multiplizieren, um die Zahl zu erhalten, die Sie bereits haben?“

Zum Beispiel:

Die Quadratwurzel von 1 ist 1, da 1 mal 1 gleich 1 ist (1 x 1 = 1).

Die Quadratwurzel von 4 ist 2, da 2 mal 2 gleich 4 ist (2 x 2 = 4).

Die Quadratwurzel von 9 ist 3, da 3 x 3 = 9.

Verwenden Sie die Division, um die Quadratwurzel zu finden

Um die Quadratwurzel einer Ganzzahl zu finden, können Sie die Ganzzahl durch aufeinanderfolgende Zahlen dividieren, bis Sie einen Quotienten finden, der genau Ihrem Divisor entspricht.

Zum Beispiel:

16 geteilt durch 4 ist 4, also ist 4 die Quadratwurzel von 16.

4 geteilt durch 2 ist 2, also ist 2 die Quadratwurzel von 4.

Finden Sie die Quadratwurzel anderer Zahlen

Raten Sie und wenden Sie dann das Ausschlussverfahren an.

Beispiel: Finden Sie die Quadratwurzel von 20.

Mittlerweile wissen wir, dass 16 eine Quadratzahl mit der Quadratwurzel 4 ist (4X4=16).

25 hat auch eine Quadratwurzel von 5 (5X5=25).

Wir würden also vermuten, dass die Quadratwurzel von 20 irgendwo zwischen 4 und 5 liegt.

Wir können annehmen, dass die Quadratwurzel aus 20 4,5 ist, und versuchen, 4,5 zu quadrieren, um dies zu überprüfen. Das heißt, wir nehmen 4,5 x 4,5. Wenn das Ergebnis nicht 20 ist, sehen wir, ob das Ergebnis größer oder kleiner als 20 ist. Ist es kleiner als 20, versuchen wir es weiter mit 4,6 und höheren Zahlen. Ist das Ergebnis größer als 20, versuchen wir es mit 4,4 und niedrigeren Zahlen, bis wir das richtige Ergebnis erhalten.

Das Ergebnis dieser Berechnung lautet 4,475 x 4,475 = 20,03. Abgerundet ergibt sich 20.

So vergleichen Sie Quadratwurzeln

Mit zwei beliebigen positiven Zahlen a und b

Wenn a = b, dann

Wenn a > b, dann

Wenn a < b="" dann="">

Zum Beispiel: 

Vergleichen und

Weil 21 < 31,

Hoffentlich hat Ihnen der obige Artikel geholfen, das Wissen über Quadratwurzeln zu verstehen, wie man rechnet, wie man vergleicht ..., Übungen zu Quadratwurzeln sowie andere damit verbundene Übungen zu lösen.