Formel zur Berechnung der Mantelfläche eines Kegels, der Gesamtfläche eines Kegels, des Volumens eines Kegels, V eines Kegels

Im folgenden Artikel stellt Quantrimang.com einige Inhalte zum Thema Formeln zur Berechnung des Volumens, der Mantelfläche und der Gesamtfläche eines Kegels vor und teilt sie mit den Lesern ausführlich. Bitte beachten Sie diesen Artikel.

Inhaltsverzeichnis

• Berechnen Sie die Fläche des Kegels
• Berechnen Sie das Volumen eines Kegels
• Bestimmen Sie den Generator, die Höhe und den Basisradius

Eine Pyramide entsteht, indem man ein rechtwinkliges Dreieck einmal um seine Achse (eine rechtwinklige Seite) dreht.

Berechnen Sie die Fläche des Kegels

Die Fläche eines Kegels wird oft mit zwei Begriffen angegeben: umgebend und gesamt.

• Die Mantelfläche eines Kegels umfasst nur die den Kegel umgebende Oberfläche, nicht die Grundfläche.
• Die Gesamtfläche errechnet sich aus der Größe der gesamten von der Figur eingenommenen Fläche, einschließlich der Mantelfläche und der Fläche der kreisförmigen Grundfläche.

Im Einzelnen wie folgt:

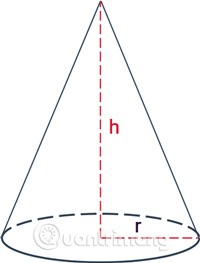
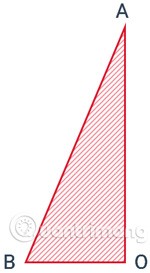
Bei einem rechtwinkligen Dreieck ABO an der Stelle O ergibt eine Drehung um die feste rechtwinklige Seite OA einen Kegel.

Die Kante OB verläuft zur Basis des Kegels, einem Kreis mit Mittelpunkt O. Kante AB überstreicht die umgebende Oberfläche des Kegels, jede ihrer Positionen wird als Generator bezeichnet, beispielsweise ist AB ein Generator. A ist der Scheitelpunkt und AO ist die Höhe des Kegels.

Formel zur Berechnung der Mantelfläche: gleich der Hälfte des Produkts aus dem Umfang des Grundkreises und der Länge der Mantellinie.

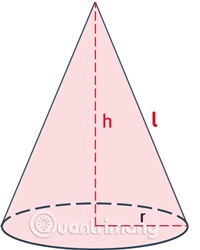
Auf das konkrete Beispiel oben angewendet: Darin: Der Umfang ist die Fläche um den Kegel. rist der Radius der Kegelbasis. list die Länge der Mantellinie des Kegels.

Formel zur Berechnung der Gesamtfläche: entspricht Seitenfläche plus Grundfläche.

Berechnen Sie das Volumen eines Kegels

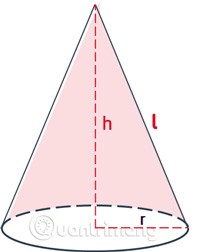
Das Volumen eines Kegels ist der Raum, den der Kegel einnimmt.

Formel zur Berechnung des Volumens eines Kegels: gleich 1/3 der Grundfläche multipliziert mit der Höhe

Darin:

• Vist das Volumen des Kegels.
• rist der Basisradius des Kegels.
• hist die Höhe, der Abstand zwischen der Spitze und der Basis des Kegels.

Bestimmen Sie den Generator, die Höhe und den Basisradius

Die Höhe ist der Abstand von der Mitte der Basis bis zur Spitze der Pyramide.

Der Generator ist die Entfernung von jedem beliebigen Punkt auf dem Grundkreis zur Spitze der Pyramide.

Da ein Kegel entsteht, wenn ein rechtwinkliges Dreieck einmal um die Achse einer seiner rechtwinkligen Seiten gedreht wird, können die Höhe und der Basisradius als die beiden rechtwinkligen Seiten des Dreiecks betrachtet werden, und die Generatorin ist die Hypothenuse.

Wenn wir die Höhe und den Basisradius kennen, können wir die Mantellinie mit der folgenden Formel berechnen:

Wenn Sie die Höhe und die Mantellinie kennen, berechnen Sie den Basisradius nach der folgenden Formel:

Oben finden Sie die Formeln zur Berechnung der Mantelfläche, der Gesamtfläche und des Volumens eines Kegels. Vielen Dank, dass Sie den Artikel verfolgt haben.